总习题三
1.填空题
（1）函数f（x）＝xln（x－1）在x＝2处的泰勒展开式中，带（x－2）3的项为.
（2）极限
（3）f（x）＝xex的4阶带拉格朗日型余项的麦克劳林公式为
（4）由拉格朗日中值定理，有
，则
（5）函数f（x）＝
在 （0，＋∞）上的极大值为
，极小值为
（6）函数f（x）＝
在区间［0，4］上的最大值为
最小值为
（7）
（tan x）tan 2x ＝
（8）
2.选择题
（1）
＝2，其中a2＋c2≠0，则必有（ ）.
（A）b＝4d （B）b＝－4d （C）a＝4c （D）a＝－4c
（2）设
＝－1，则在x＝1处（ ）.
（A）f（x）的导数存在，且f′（a）≠0 （B）f（x）取得极大值
（C）f（x）取得极小值 （D）f（x）的导数不存在
（3）f（x）有二阶连续导数，且f′（0）＝0，
＝1，则（ ）.
（A）f（0）是f（x）的极大值
（B）f（0）是f（x）的极小值
（C）（0，f（0））是曲线y＝f（x）的拐点
（D）f（0）不是f（x）的极值，（0，f（0））不是曲线y＝f（x）的拐点
（4）曲线y＝（x－1）2（x－3）2的拐点的个数为（ ）.
（A）0 （B）1 （C）2 （D）3
（5）曲线y＝
arctan
的渐近线有（ ）.
（A）1条 （B）2条 （C）3条 （D）4条
3.已知f（x）在（－∞，＋∞）内可导，且
4.证明不等式：
5.设f（x）在区间［0，1］上连续，在（0，1）内可导，且f（0）＝f（1）＝0，f （
）＝1.证明：
（1）存在η∈（
，1）使f（η）＝η；
（2）对任意实数λ，必存在ξ∈（0，η），使f′（ξ）－λ［f（ξ）－ξ］＝1.
6.设f（x）可导，证明f（x）的两个零点之间一定有f′（x）－af（x）的零点（a为常数）.
7.设函数f（x）在闭区间［－1，1］上具有三阶连续导数，且f（－1）＝0，f（1）＝1，f′（0）＝0.证明：在开区间（－1，1）内至少存在一点ξ，使f‴（ξ）＝3.
8.讨论函数在x＝0处的连续性：
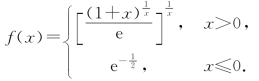
9.设在［0，1］上，f″（x）＞0，证明f′（1）＞f（1）－f（0）＞f′（0）.
10.两个正数a与b的乘积为实数c，求am＋bn（m，n＞）的最小值.
11.求数列
的最大项.
12.证明曲线y＝
有三个拐点位于同一直线上.
13.求曲线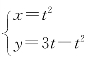
的拐点.
14.求曲线y＝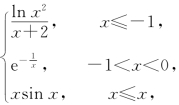
的渐近线.
15.设f（x）在［a，＋∞）内二阶可导，且f（a）＞0，f′（a）＜0，f″（x）＜0（x＞a），证明：方程f（x）＝0在（a，＋∞）内有且仅有一实根.
16.设函数f（x）在［0，1］上有三阶导数，且f（0）＝f（1）＝0.设F（x）＝x3 f（x），试证在（0，1）内存在一点ξ，使得F‴（ξ）＝0.
17.若f（x）在［a，b］上连续，在（a，b）内可导，a＞0.求证：存在ξ，η∈（a，b），使f′（ξ）＝
（a＋b）.
18.设f（x）在［0，1］上二阶可导，f（0）＝f（1），f′（1）＝1，求证：∃ξ∈（0，1），使得f″（ξ）＝2.
19.设f（x）在［a，b］上连续，在（a，b）内可导，且f（a）＝f（b）＝1.证明：存在ξ，η∈（a，b），使得eη－ξ［f（η）＋f′（η）］＝1.
20.讨论方程ex＝ex＋b的实根的个数.