一、微分的概念
前面讨论了导数的概念与求导法则.导数是函数的增量与自变量增量之比的极限,而并非增量本身.在实际问题中,经常涉及当自变量发生微小变化时,求函数值相应的变化问题.先考察一个具体问题.
一边长为x的正方形铁片,受热胀冷缩的影响,边长会有改变.设边长的改变量为Δx,则铁片的面积S=x2也有相应的改变量ΔS,且
ΔS=(x+Δx )2-x2=2xΔx+(Δx )2,
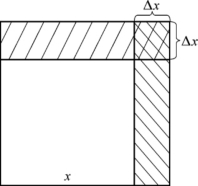
图2-4
此处,ΔS被分成两部分,第一部分2xΔx是Δx的线性函数,即图2-4中画斜线的那两个矩形面积之和;第二部分(Δx)2是关于Δx的高阶无穷小量,即(Δx)2=o(Δx)(Δx→0),如图2-4所示网状线部分.由此知,当边长发生微小改变量Δx时,它所引起的面积的改变量ΔS可近似地用第一部分2xΔx代替,由此所产生的误差仅是(Δx)2,它与2xΔ相比微乎其微,此时
ΔS≈2xΔx.
推广到一般情形,有如下定义.
定义1 设函数y=f(x)在某区间内有定义,当x的改变量为Δx时,若函数的改变量为
Δy=f (x+Δx)-f(x)=AΔx+o(Δx),
其中,A是x的函数而与Δx无关,则称f(x)在点x可微,AΔx是f(x)在点x的微分,记为dy或df(x),即
dy=AΔx.
由于AΔx是Δx的线性函数,且当Δx→0时,Δy≈AΔx,称AΔx为Δy的线性主部,也就是说,dy是Δy的主要部分.
为了方便起见,规定自变量x的改变量Δx为自变量的微分,记作dx,即
dx=Δx,
于是,函数y=f(x)的微分为
dy=Adx.
例1 已知圆的半径为r,面积为S=πr2,求当半径增大Δr时,圆面积的增量ΔS及微分dS.
解 圆面积的增量为
ΔS=π(r+Δr )2-πr2=2πrΔr+π(Δr )2,
易知,2πrΔr是ΔS的线性主部,而π(Δx)2是Δr的高阶无穷小量,故有
dS=2πrΔr=2πrdr.
若函数y=f(x)在点x可微,是否都要通过计算增量而得到其线性主部AΔx?是否还有其他方法?
定理1 函数y=f(x)在点x可微的充分必要条件是y=f(x)在点x可导,且有
dy=f′(x)dx.
证 必要性.
因为函数y=f(x)在点x可微,所以
Δy=AΔx+oΔ(x),
其中,A与Δx无关.上式两边除以Δx,则
![]()
两边取极限,令Δx→0,有
![]()
即y=f(x)在点x可导,且f′(x)=A.
此时函数y=f(x)的微分:dy=Adx=f′(x)dx.
充分性.
由于y=f(x)在点x可导,有
![]()
即
![]()
从而有
Δy=f′(x)Δx+αΔx=f′(x)Δx+oΔ(x),
式中,f′(x)显然与Δx无关,而o(Δx)=αΔx是Δx的高阶无穷小量.由函数微分的定义知,y=f(x)在点x可微,且
dy=f′(x)dx.
由此可见,函数y=f(x)在点x处可导与可微是等价的.
例2 设y=ln(1+2x),求dy,dy|x=1.
解 因为
![]()
所以
![]()
当x=1时,
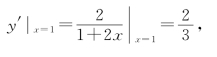
此时
![]()
