习题2－1

习题2－1

1.高温物体在空气中会逐渐冷却，在此过程中温度T是时刻t的函数，即T＝f（t）.试给出下列概念的定义：

（1）从时刻t0到时刻t0＋Δt这段时间内空气冷却的平均速度；

（2）在时刻t0的冷却速度.

2.一质点作变速直线运动，其路程函数s＝3t2＋1，求时刻t＝2时的瞬时速度.

3.设函数f（x）在x0处可导，试用导数f′（x0）表示下列极限.

4.求下列函数的导数.

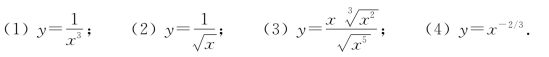
5.求下列曲线在指定点处的切线方程和法线方程.

（1）y＝ex在点（0，1）处；　　（2）y＝在点（1，1）处.

6.设曲线方程为y＝，试求：

（1）曲线在点（4，8）处的切线方程和法线方程；

（2）求曲线的切线，使它与直线6x－y＝5平行.

7.设f（x）为偶函数，且在点x＝0可导，证明f′（0）＝0.

8.证明：

（1）可导奇函数的导函数是偶函数；

（2）可导偶函数的导函数是奇函数；

（3）可导周期函数的导函数仍为周期函数.

9.讨论下列函数在x＝0处的连续性和可导性.

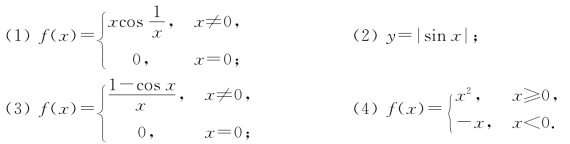
10.证明：双曲线xy＝a2（a＞0）上任一点处切线与两坐标轴构成的三角形的面积等于常数2a2.