最大值、最小值定理

一、最大值、最小值定理

定理1 若函数f（x）在闭区间［a，b］上连续，则f（x）在［a，b］上一定取得最大值M和最小值m，即存在两点x1，x2∈［a，b］（见图1－21），使得

且对∀x∈［a，b］，有

例如，y＝sin x在［0，π］上连续，其最小值为0，在两点x＝0，x＝π上取得，最大值1在点x＝取得.

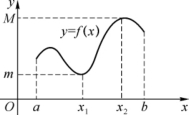
图1－21

一般而言，若函数在非闭区间上连续，或在闭区间上有间断点，那么不能保证函数在此区间上有最大值和最小值.

例如，y＝在（0，1）上连续，但y＝在（0，1）既无最大值又无最小值.

又如函数

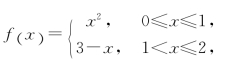
它在［0，2］上不连续，有间断点x＝1（见图1－22），f（x）在［0，2］上有最小值0，无最大值.

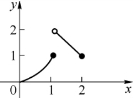
图1－22

推论1 （有界性定理） 若函数f（x）在闭区间［a，b］上连续，则f（x）在［a，b］上有界.