无穷小量的概念
1.无穷小量的概念
定义1 设函数f(x)在点x0的某个邻域内有定义,如果对任意给定ε>0,∃δ>0,当0<![]() <δ时,有
<δ时,有![]() <ε,则称函数f(x)是当x→x0时的无穷小量,记作
<ε,则称函数f(x)是当x→x0时的无穷小量,记作
![]()
此外,可类似定义在x的其他趋向下的无穷小量.
例1 因为![]() x=0,所以函数f(x)=x是当x→0时的无穷小量;又如
x=0,所以函数f(x)=x是当x→0时的无穷小量;又如![]() =0,所以函数f(x)=
=0,所以函数f(x)=![]() 是当x→∞时的无穷小量;极限
是当x→∞时的无穷小量;极限![]() ex=0,所以函数f(x)=ex是当x→-∞时的无穷小量.
ex=0,所以函数f(x)=ex是当x→-∞时的无穷小量.
对于无穷小量的概念,需要注意:
(1)无穷小量是描述函数当自变量在某一变化过程中函数值的绝对值越来越小的术语.因此,无穷小量是一变量,不是绝对值很小的数.零是作为无穷小量的唯一的一个常数.
(2)一个变量是否为无穷小量与自变量的变化趋向有关.如f(x)=x是当x→0时的无穷小量;当x→1时,它的极限是“1”而不是“0”,也就是当x→1时,f(x)=x不是无穷小量.
无穷小量和一般函数极限之间有什么关系呢?
定理1 在自变量的某一变化过程中,设f(x)=A+α(x),A是不为零的常数.若limf(x)=A,则limα(x)=0;反之亦然.
证 不妨设![]() f(x)=A,则由函数极限的定义知:对∀ε>0,∃δ>0,当0<
f(x)=A,则由函数极限的定义知:对∀ε>0,∃δ>0,当0<![]() <δ时有
<δ时有
![]()
即
![]()
反之,若![]() α(x)=0,由于f(x)=A+α(x),所以对∀ε>0,∃δ>0,当0<
α(x)=0,由于f(x)=A+α(x),所以对∀ε>0,∃δ>0,当0<![]() <δ时有
<δ时有
![]()
故有
![]()
由定理1可知:若在某种趋向下函数f(x)有极限A,则该函数f(x)必可写成极限值A与该趋向下的一个无穷小量α(x)的和.
例2 设f(x)=![]() ,当x→∞时和x→0时,分别把f(x)写成f(x)=A+α(x)的形式.
,当x→∞时和x→0时,分别把f(x)写成f(x)=A+α(x)的形式.
解 (1)因为![]() f(x)=2,所以
f(x)=2,所以
![]()
且
![]()
故有
![]()
(2)![]() f(x)=
f(x)=![]() =-1,所以
=-1,所以
![]()
且
![]()
故有
![]()
2.无穷大的概念
如果自变量趋向于某个值时,函数f(x)的绝对值![]() 无限增大,则称f(x)是该趋向下的无穷大量.
无限增大,则称f(x)是该趋向下的无穷大量.
定义2 若对∀M>0,总∃δ>0,当0<![]() <δ时,恒有
<δ时,恒有
![]()
成立,则称函数f(x)是当x→x0时的无穷大量,记作
![]()
注意 当x→x0时函数f(x)是无穷大量,此时f(x)的极限不存在,它只是极限不存在的一种特殊情形.
无穷大量又分为正无穷大量和负无穷大量,其精确定义可类似给出.
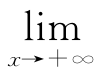 f(x)=+∞:∀M>0,∃X>0,当x>X时,f(x)>M;
f(x)=+∞:∀M>0,∃X>0,当x>X时,f(x)>M;
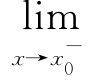 f(x)=-∞:∀M>0,∃δ>0,当x0-δ<x<x0时,f(x)<-M.
f(x)=-∞:∀M>0,∃δ>0,当x0-δ<x<x0时,f(x)<-M.
例3 用定义证明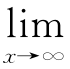 xn=∞,n为正整数.
xn=∞,n为正整数.
证 对于∀M>0(不妨取M>1),要使
![]()
只要
![]()
取X=![]() ,则当
,则当![]() >X时,有
>X时,有![]() >M,即
>M,即
![]()
例4 用定义证明![]() =∞.
=∞.
证 因为要考虑函数在x=1的邻域内的变化情况,不妨设0<x-1<1,即0<x<2(x≠1),此时
![]()
对于∀M>0,要使![]() >M,只要
>M,只要
![]()
即
![]()
取δ=min![]() ,则当0<
,则当0<![]() <δ时,恒有
<δ时,恒有![]() >M成立.
>M成立.
即
![]()
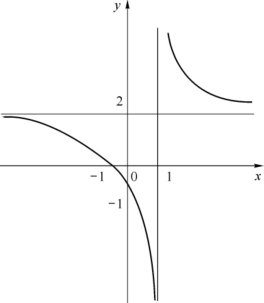
图1-18
由图1-18可知,当x→1-时,![]() 是负无穷大量;当x→1+时
是负无穷大量;当x→1+时![]() 是正无穷大量.
是正无穷大量.
注意无穷大量与无界函数的区别,如函数f(x)=xsin x在(0,+∞)上无界,但当x→+∞时,f(x)=xsin x不是无穷大量.
注意 此处关于无穷小量、无穷大量讨论的结论对数列同样成立.
定理2 在自变量的同一变化趋向下,若函数f(x)为无穷大量,则![]() 为无穷小量;反之,若f(x)为无穷小量,且f(x)≠0,则
为无穷小量;反之,若f(x)为无穷小量,且f(x)≠0,则![]() 为无穷大量.
为无穷大量.
证 设![]() f(x)=∞,对于∀ε>0,取M=
f(x)=∞,对于∀ε>0,取M=![]() ,则∃δ>0,当0<
,则∃δ>0,当0<![]() <δ时,有
<δ时,有
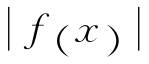 >M,此时
>M,此时![]() =ε,即有
=ε,即有![]() =0.
=0.
证明的另一部分请读者自行完成.
下面是几个常用的无穷小量与无穷大量:
由![]() xn=∞,得
xn=∞,得![]() =0;
=0;
由![]() =+∞,得
=+∞,得![]() e-x=0;
e-x=0;
由![]() =+∞,得
=+∞,得![]() =0.
=0.
