二阶常系数线性微分方程实例
例1(振动问题) 设有一个弹簧,它的上端固定,下端挂一个质量为m的物体,当物体处于静止状态时,作用在物体上的重力与弹力大小相等、方向相反,这个位置就是物体的平衡位置,如图6-3所示.取y轴竖直向下,并取物体的平衡位置为坐标原点.推导物体以初速度v0在平衡位置上下振动时,分别不受和受竖直干扰力作用下的微分方程式.
解 设在振动过程中,物体位置y随时间t变化的函数形式为y=y(t).
由力学的胡克定律知,弹簧使物体回到平衡位置的弹力和物体离开平衡位置的位移y成正比,即
![]()
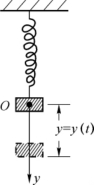
图6-3
其中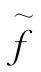 为弹力,k为弹簧的弹性系数,负号表示弹力方向和物体位移的方向相反.
为弹力,k为弹簧的弹性系数,负号表示弹力方向和物体位移的方向相反.
另外,物体在运动过程中还受到阻尼介质(如空气,油等)的阻力作用,使振动逐渐消耗能量而趋于停止.这种阻力总与运动方向相反,当振动不大时,其大小与物体的速度![]() 成正比,设比例系数为μ,则阻力fμ满足
成正比,设比例系数为μ,则阻力fμ满足
![]()
由上述受力分析,按牛顿第二定律得
![]()
移项整理,并记![]() =p
=p![]() =q.上式化简为
=q.上式化简为
![]()
这就是物体不受外力干扰,但在有阻尼的情况下,物体自由振动的微分方程.
若物体在振动过程中还受到竖直干扰力F=F(t)的作用,则按牛顿第二定律有
![]()
若记
![]()
则方程化为
![]()
这就是物体强迫振动时的微分方程.
注意 方程(1)和方程(2)的系数p和q与时间t无关,称它们是常系数线性微分方程.
下面再解决一个电路的问题.
例2 如图6-4所示是含有自感L、电阻R与电容C(其中R,L和C是常数)的闭合电路,接入电动势E=E(t)的电源,推导电路中任何时刻电流i(t)的方程式.
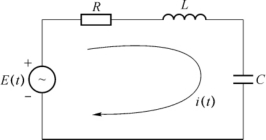
图6-4
解 由基尔霍夫第二定律知,回路电压降的代数和等于接入回路的电动势.
电流在电阻上的电压降为Ri,电流在电容上的电压降为![]() Q(Q为电容器两极板间的电容量),电流在电感上的电压降为L
Q(Q为电容器两极板间的电容量),电流在电感上的电压降为L![]()
于是,有
![]()
为消去方程中的电容量变量Q,利用![]() =i,可将上式两端对t求导,得
=i,可将上式两端对t求导,得
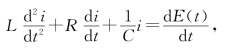
令p=![]() =f(t),得到i=i(t)的微分方程
=f(t),得到i=i(t)的微分方程
![]()
上述三个方程(1)、(2)和(3)的共同特点是二阶常系数线性方程.求解此类方程对进一步研究物理和电路问题不可或缺.更复杂的实际情况留在数学物理方程课中继续讨论.
下面首先讨论二阶常数齐次线性方程的解法.
