总习题六
1.填空题
（1）一阶线性微分方程y′＋P（x）y＝Q（x）的通解为
（2）如果函数y1，y2，…，yn是n阶线性齐次方程y（n）＋Pn（x）y（n－1）＋…＋P1（x）y＝0的n个线性无关的解，则该方程的通解为y＝
（3）若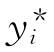
是n阶线性非齐次方程
的特解，则方程y（n）＋Pn（x）y（n－1）＋…＋P1（x）y＝
（x）的特解为
（4）以y1＝sin x，y2＝cos x为特解的最低阶常系数齐次线性方程是
（5）微分方程y″－5y′＋6y＝exsin x＋6的一个特解形式为y＊＝
（6）已知y＊是y″－2y′－3y＝f（x）的一个特解，则此方程的通解为y＝
（7）曲线y＝f（x）过点（0，－
），且其上任一点（x，y）处的切线斜率为xln（1＋x2），则f（x）＝
2.选择题
（1）方程（x＋1）（y2＋1）dx＋y2 x2dy＝0是（ ）.
（A）齐次方程 （B）可分离变量方程
（C）伯努利方程 （D）线性非齐次方程
（2）已知f（x）＝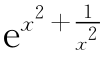
，g（x）＝
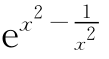，h（x）＝e（
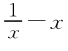）2，则（ ）.
（A）f（x）与g（x）线性相关 （B）g（x）与h（x）线性相关
（C）f（x）与h（x）线性相关 （D）任意两个都线性相关
（3）求方程（x＋1）y″＋y′＝ln（x＋1）的通解时，可（ ）.
（A）令y′＝P，则y″＝P′ （B）令y′＝P，则y″＝P
（C）令y′＝P，则y″＝P
（D）令y′＝P，则y″＝P′
（4）在下列微分方程中，以y＝C1ex，C2cos 2x，C3sin 2x（C1，C2，C3为任意常数）为通解的是（ ）.
（A）y‴＋y″－4y′－4y＝0 （B）y‴＋y″＋4y′＋4y＝0
（C）y‴－y″－4y′＋4y＝0 （D）y‴－y″＋4y′－4y＝0
3.设F（x）＝f（x）g（x），其中函数f（x），g（x）在（－∞，＋∞）内满足以下条件：
f′（x）＝g（x），g′（x）＝f（x），且f（0）＝0，f（x）＋g（x）＝2ex.
（1）求F（x）所满足的一阶微分方程；
（2）求出F（x）的表达式.
4.设函数y＝y（x）在（－∞，＋∞）内具有二阶导数，且y′≠0，x＝x（y）是y＝y（x）的反函数.则
（1）试将x＝x（y）所满足的微分方程
＋（y＋sin x）（
）3＝0变换为y＝yx满足的微分方程.
（2）求变换后的微分方程满足初始条件y（0）＝0，y′（0）＝
的解.
5.设单位质点在水平面内作直线运动，初速度v｜t＝0＝v0，已知阻力与速度成正比（比例常数为1），问t为多少时此质点的速度为
.并求到此时刻该质点所经过的路程.
6.设函数f（x）在区间［1，＋∞）内连续，由y＝f（x），x＝1，x＝t（t＞1）及x轴围成的平面图形绕x轴旋转一周所成的旋转体体积V（t）＝
［t2 f（t）－f（1）］，求函数f（x）所满足的微分方程，并求该微分方程满足初始条件y｜x＝2＝
的特解.
7.函数f（x）在［0，＋∞）上可导，f（0）＝1，且满足等式
（1）求导数f′（x）；
（2）证明：当x≥0时，不等式e－x ≤f（x）≤1成立.
8.设函数f（x）在闭区间［0，1］上连续，在开区间（0，1）内大于零，并满足xf′（x）＝f（x）＋
（a为常数），又由线y＝f（x）与x＝1，y＝0所围的图形S的面积值为2，求函数y＝f（x）.并问a为何值时，图形S绕x轴旋转一周所得的旋转体的体积最小.
9.某湖泊的水量为V，每年排入湖泊内含污染物A的污水量为
，流入湖泊内不含A的水量为
，流出湖泊的水量为
.已知1999年年底湖中A的含量为5m，超过国家规定指标.为了治理污染，从2000年年初起，限定排入湖泊中含A污水的浓度不超过
.问至多需经过多少年，湖泊中污染物A的含量降至m0以内？（注：湖泊中A的浓度是均匀的）.
10.设函数f（x）在［0，＋∞）上可导，f（0）＝0，且其反函数为g（x）.若
g（t）dt＝x2ex，求f（x）.