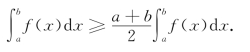二、定积分的性质
此处略去讨论函数的可积性，假定以下性质中所有定积分都存在.
性质1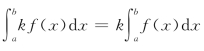
，（k为常数）.
证 由于
存在，从而由定积分的定义，有
于是
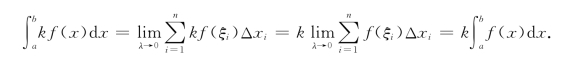
由此不难证明性质2.
性质2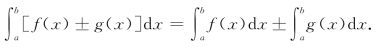
实际上，用定积分的定义可证明如下线性性质：
性质3 设a＜c＜b，则
证 由于f（x）在［a，b］上可积，可选取特殊分割，使c永远是个分点.这样，区间［a，b］上的积分和就等于区间［a，c］与［c，b］上的积分和之和，即
从而，当全分割细度λ→0利用定积分的性质，便有
性质3称为定积分关于积分区间的可加性.其几何意义就是曲边梯形面积的可加性.
实际上，若c＜a＜b或a＜b＜c，同样有
这是由于（不妨设a＜b＜c）对上式右端第一项利用积分区间可加性，有
性质4 若在区间［a，b］上，f（x）＝1，则
证
性质5 若在区间［a，b］上，f（x）≥0，则
证 由于f（x）≥0，从而任何分割的介点集的函数值
f（ξi）≥0 （i＝1，2，…，n），
则有
推论1 若在区间［a，b］上，f（x）≤g（x），则
证 由于g（x）－f（x）≥0，由性质5得
即
移项便得待证的不等式.
推论2
证 由于
－｜f（x）｜≤f（x）≤｜f（x）｜，
则由以上性质，有
即
应用此性质时，一定要注意，不等式是在积分下限小于积分上限时才成立，否则不等号方向正好相反.
性质6 若M与m分别为f（x）在［a，b］上的最大值与最小值，则
证 由于m≤f（x）≤M，有
又
＝m（b－a），类似有
＝M（b－a），从而有
这个性质又称为估值定理，当f（x）≥0时，其几何意义是指曲边梯形的面积介于两个矩形面积之间（见图5－6）.利用此性质可大致估计积分值的范围.
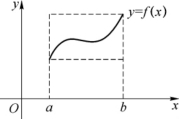
图5－6
性质7（积分中值定理） 若f（x）在闭区间［a，b］上连续，则在［a，b］上至少存在一点ξ，使得
证 由闭区间上连续函数的性质知，f（x）在［a，b］内必有最大值M与最小值m，即
m≤f（x）≤M，x∈［a，b］.
由性质6知
从而有
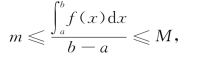
再由闭区间上连续函数的介值定理知，至少存在一点ξ∈［a，b］，使得
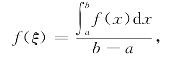
即
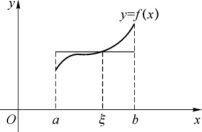
图5－7
如图5－7所示，当f（x）非负时，积分中值定理的几何意义是指曲边梯形的面积等于以f（ξ）为高，［a，b］为底的矩形面积.f（ξ）＝
称为函数f（x）在区间［a，b］上的平均值，是有限个数算术平均值的推广.
性质8 若f（x）在［a，b］上连续，g（x）在［a，b］上可积且不变号，则至少存在一点ξ∈［a，b］，使得
证 因g（x）不变号，不妨设g（x）非负，且设M，m分别为连续函数f（x）在［a，b］上的最大值与最小值.这时，有
从而有
若
＝0，则由式（4）知，
（x）g（x）dx＝0.这样，ξ取［a，b］内任何值均使式
（3）成立.
若
（x）dx＞0，由式（4）得
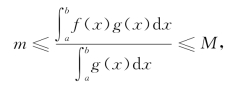
再由连续函数介值定理，至少存在一点ξ∈［a，b］，使得因此式（3）成立.
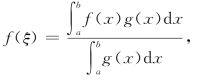
通常将此性质称为积分第一中值定理.
当g（x）＝1（x∈［a，b］）时，此性质便是积分中值定理.
例2 利用积分估值定理证明不等式
证 设f（x）＝
，由于f（x）在［e，4e］上连续，下面求f（x）在［e，4e］上的最大值与最小值.
由f′（x）＝
＝0得f（x）在［e，4e］上的唯一驻点为x＝e2.
在区间［e，e2］上，有f′（x）＞0，则函数f（x）单调递增；在区间［e2，4e］上，有f′（x）＜0，则函数f（x）单调递减.
因此，x＝e2为极大值点，也为最大值点，最大值f（e2）＝
.又f（4e）＝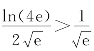
＝f（e），故f（e）＝
为最小值.因此，在区间［e，4e］上，
，由此得
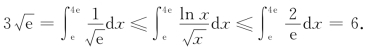
例3 设f（x）在［0，1］上连续且单调递减.证明，当0＜λ＜1时，
≥
证 将右端积分区间拆为［0，λ］与［λ，1］，由于f（x）连续，因此利用积分中值定理，并注意到f（x）的单调性，有
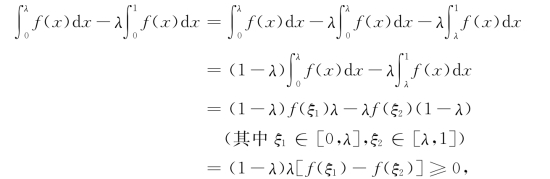
从而有
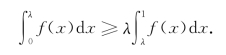
例4 设f（x）在闭区间［a，b］上连续，且单调递增.证明
证 由于f（x）在［a，b］上连续，故将积分区间拆成
，再分别利用积分第一中值定理，并注意函数f（x）的单调性与定积分的几何意义，有
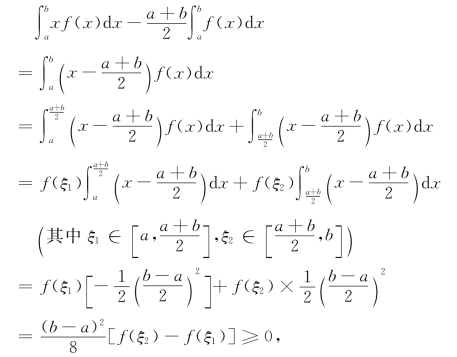
从而有
