数列极限的定义

一、数列极限的定义

如果按某个规则把无穷多个数按一定次序排成一列，即

x1，x2，…，xn，…，

则称这一列数为无穷数列，简称为数列，记作｛xn｝（有时也记为xn），数列中的每一个数称为数列的一个项，带有下标n的第n项xn称为数列的一般项或通项.例如，

（1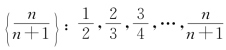），…，通项为；

（2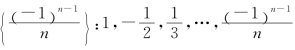），…，通项为

（3）｛（－1）n－1｝：1，－1，1，－1，…，（－1 ）n－1，…，通项为（－1 ）n－1；

（4）：sin 1，2sin，3sin，…，nsin，…，通项为nsin；

（5）｛2n｝：2，22，…，2n，…，通项为2n.

仔细观察可以发现：随着n的增大，有的数列无限增大，有的数列跳跃不定，有的数列无限接近于一个常数a.这种无限接近于一个常数a的数列称为有极限的数列，a称为此数列的极限.如随着n的增大，数列无限接近于常数1，即与1的差的绝对值越来越小.又如，随着n的增大，数列无限接近于常数0，与0的差的绝对值越来越小.此处的“越来越小”为：不论给定多么小的正数ε，总可以取充分大的n，使得＜ε成立.

定义1 设｛xn｝为一数列，a为常数，如果对任意给定的ε＞0，总存在一个正整数N，当n＞N时，不等式

恒成立，则称数列｛xn｝的极限存在，并称常数a为数列｛xn｝的极限，记作

此时也称数列｛xn｝收敛.不收敛的数列称为发散数列，或数列发散.

由数列极限的定义知：去掉或改变数列｛xn｝的有限项，不改变其收敛性或发散性.

数列极限的定义常用逻辑符号表述为：∀ε＞0，∃N＞0，当n＞N时，恒有

成立.

数列极限的几何意义：将常数a及数列x1，x2，…，xn，…在数轴上用它们的对应点表示出来，再在数轴上作以a为中心且以ε为半径的邻域（a－ε，a＋ε），当n＞N时，所有的点xn都落在该邻域内，如图1－11所示.

图1－11

例1 用定义证明＝2.

证 对∀ε＞0，要使

只要

取N＝，则当n＞N时，不等式

恒成立，由定义知

例2 证明＝0（0＜q＜1）.

证 对于∀ε＞0，要使

只要

nln q＜lnε，

即

取N＝，则当n＞N时，有

即

例3 证明＝0（a＞1）.

证 因为

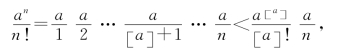
记c＝（显然，c是一常数），此时要使＜ε，只要＜ε，即

取N＝，则当n＞N时，有

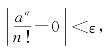
即

注意 在极限的定义中关心的不是N的具体值，而是N是否存在.所以，实际证明的过程不必精确地求出N，通过适当地放大不等式，可以更容易地说明N存在.