二、基本积分表

二、基本积分表

以下要解决的问题是如何求原函数.由于初等函数在其定义区间上均有原函数，先从求基本初等函数的原函数出发，结合一些积分法则，就可以解决初等函数求原函数的问题.读者很快会发现积分比求导要困难得多.

基本求导公式改写为基本积分公式：

（1）∫kdx＝kx＋C（k为常数）；

（2）∫xαdx＝＋C，（α≠－1，x＞0）；

（3）＝ln｜x｜＋C；

（4）＝arctan x＋C；

（5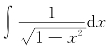）＝arcsin x＋C；

（6）∫cos xdx＝sin x＋C；

（7）∫sin xdx＝－cos x＋C；

（8）∫sec2 xdx＝tan x＋C；

（9）∫csc2 xdx＝－cot x＋C；

（10）∫sec xtan xdx＝sec x＋C；

（11）∫csc xcot xdx＝－csc x＋C；

（12）∫exdx＝ex＋C；

（13）∫axdx＝＋C （a＞0，a≠1）.

在公式（3）中，x≠0.当x＞0时，（ln｜x｜）′＝（ln x）′＝

当x＜0时，（ln｜x｜）′＝［ln（－x）］′＝－，即x≠0时，（ln｜x｜）′＝