一、换元积分法
有一些不定积分，只需将积分变量进行一定变换就可用基本积分公式求出所需的积分.例如，求∫sin2 xcos xdx，由于dsin x＝cos xdx，从而被积表达式
sin2 xcos xdx＝sin2 xd（sin x）.
令u＝sin x，则以上积分变为
这就利用基本积分公式求出了积分，再将u换回sin x便求出不定积分，即
以上方法的关键在于将被积函数的因子cos x与dx凑成微分
cos xdx＝（sin x）′dx＝d（sin x），
而被积函数剩下的因子正好为sin x的函数，若将sin x视为整体.变换后的积分正好可用已有积分公式求出，这种积分公式称为“凑微分”法，也称为第一换元积分法.相关的定理如下所述.
定理1（第一换元积分法） 若∫f（u）du＝F（u）＋C，则当u＝φ（x）为连续可微函数时，有
∫f［φ（x）］φ′（x）dx＝∫f［φ（x）］dφ（x）＝∫f（u）du＝F（u）＋C＝F［φ（x）］＋C.
证
则
∫f［φ（x）］φ′（x）dx＝F［φ（x）］＋C.
例1 求∫tan xdx∫，cot xdx.
解
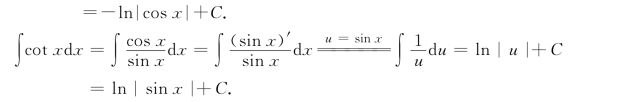
为了简便计算，在熟练的情况下，可以省去引入变量u的过程.
例2 求∫sec xdx∫，csc xdx.
解 （方法一）
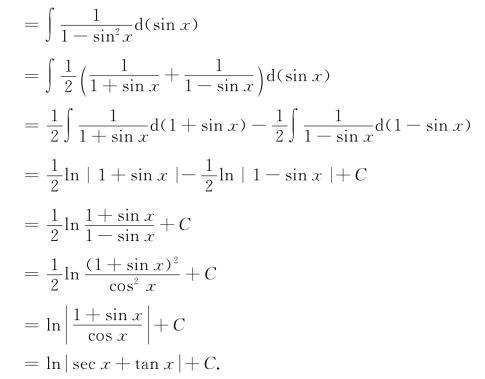
（方法二）
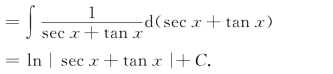
类似可求得
例3 求
解
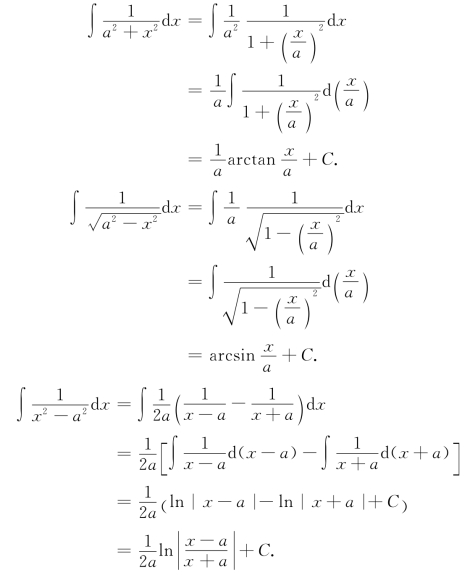
例4 求∫sin2 xdx∫，sin3 xdx.
解
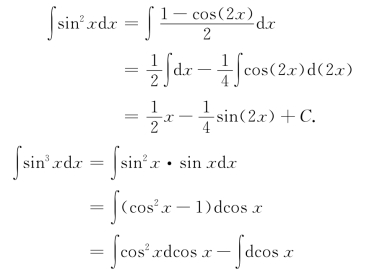
例5 求
解
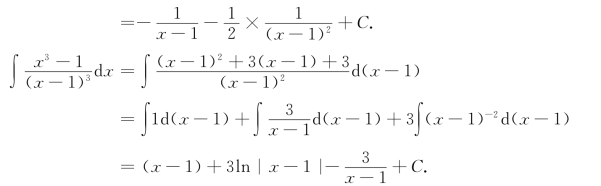
例6 求
解
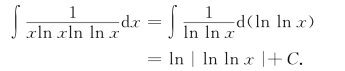
凑微分法利用如下的公式进行求解：
将此公式倒用就是第二换元积分法.
定理2（第二换元积分法） 设不定积分∫f（x）dx存在，x＝x（t）连续可微且存在反函数t＝t（x）.又若∫f［x（t）］x′（t）dt＝F（t）＋C，则
证
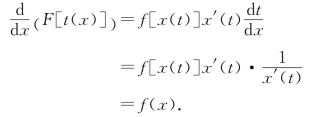
例7 求
解 设
＝t，则x＝t6，dx＝6t5dt.
则
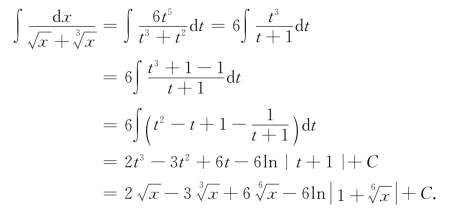
例8 求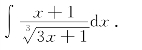
解 设
＝t，则x＝
（t3－1），dx＝t2dt.
从而有
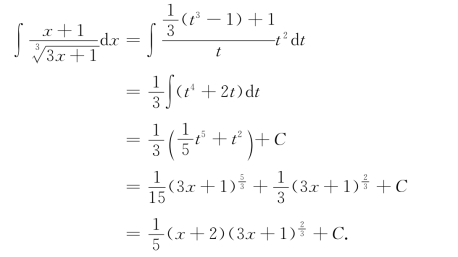
例9 求
（a＞0）.
解 设x＝asint，｜t｜＜
（此函数在这个区间内单调，存在反函数）.于是
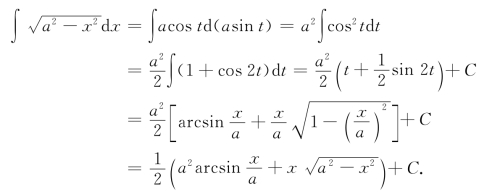
本题的关键是利用公式sin2 x＋cos2 x＝1代去被积函数的根式.类似的情形还有用公式1＋tan2 x＝sec2 x处理被积函数的方法，称此类方法为三角函数变换法，是特殊的第二换元积分法，此方法常用于被积函数含有x2±a2，a2－x2的积分中.
例10 求∫
（a＞0）.
解 设x＝atant，｜t｜＜
，于是
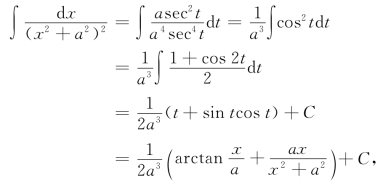
计算中可借助图4－1求出
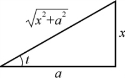
图4－1
例11 求∫
（a＞0）.
解 设x＝asec t，0＜t＜
（当－
＜t＜0时，可得同样结论），于是
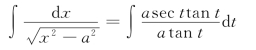
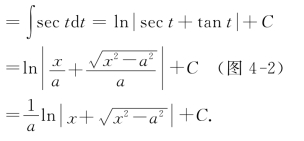
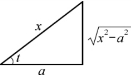
图4－2
例12 求∫
解 （方法一） 设x＝
，则dx＝－
dt.于是
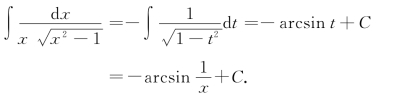
这种方法称为“倒代换”，也是一种常用的变量代换.
（方法二） 设x＝sec t，则dx＝sec ttantdt.于是
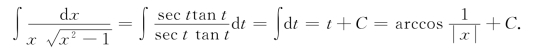
此题也可用凑微分法来解.
（方法三）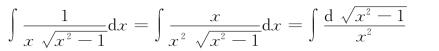
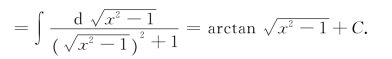
计算不定积分时，一题多解比较常见.一般而言，常规的方法往往不是最简便的，这就需要读者在学习过程中多总结经验，寻求简单巧妙的积分法.还需指出的是，应用不同的积分方法算出的答案表面上看可能不同，这是由于不同的原函数加上任意常数构成了不定积分的缘故.虽然原函数不同，实际上它们彼此只相差一个常数，它们的导数都是被积函数.所以，读者要养成用求导运算来检验不定积分的结果是否正确的好习惯.