一阶线性微分方程

一、一阶线性微分方程

型如

的方程称为一阶线性微分方程.如果Q（x）≡0，则方程（1）称为齐次方程；如果Q（x）不恒等于零，则方程（1）称为非齐次方程.

对应于非齐次方程（1）的齐次线性方程为

由分离变量法得其通解为

其中C任意常数.

下面用常数变易法求非齐次线性方程（1）的通解.

把方程（2）的通解（3）中任意常数C看作是x的未知函数C（x），假设

是非齐次线性方程（1）的解.将（4）式两边对x求导，得

把（4）式和（5）式代入方程（1）中，得

即

或

积分得

将C（x）代入（4）式，得

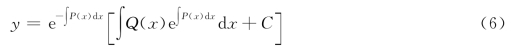
为方程（1）的通解.

注意 通解式（6）在解决物理或电路问题时起重要的作用，应熟记.另外，不定积分∫P（x）dx与∫Q（x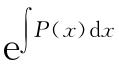dx分别理解为某个确定的原函数.

若把（6）改写为

则（7）式的第一项为齐次线性方程通解，第二项为非齐次线性方程特解（通解中取C＝0时可得）.由此可得一阶非齐次线性微分方程的通解等于对应齐次线性方程的通解与非齐次线性方程的一个特解之和.

例1 解方程xy′＋y＝x2＋3x＋2.

解 化原方程为一阶线性方程标准形为

其中P（x）＝，Q（x）＝x＋＋3，由（6）式，得通解为

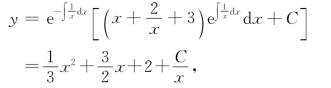
其中C为任意常数.

例2 设降落伞从跳伞塔下降后，所受空气阻力与速度成正比，并设降落伞离开跳伞塔时（t＝0时）速度为零.求降落伞下落速度与时间的函数关系，并求它的极限速度.

解 设降落伞下降速度为v＝v（t），由牛顿第二定律F＝ma知

依题意即有

由（6）式，可得方程（8）的通解为

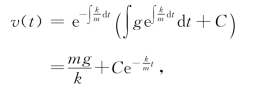
其中C为任意常数.

把（9）式代入上式，求得C＝－

因此，降落伞下落速度与时间的关系为

令t→＋∞，有

由此可见，随着t增大，速度v（t）接近常数，且不超过.即降落伞开始下降时是加速运动，以后逐渐接近匀速运动.