二阶常系数齐次线性方程通解的求法
考虑二阶常系数齐次线性方程
其中p，q是常数.
由第六节讨论知，要求（4）式的通解，只需求其两个线性无关的特解即可.
由于一阶齐次线性方程有指数形式解，且当r为常数时，指数函数y＝erx的各阶导数同它只相差一个常数因子.因此不妨用y＝erx尝试，看能否选择出适当的r使之成为方程（4）的特解.
将y＝erx代入方程（4），得
（r2＋pr＋q）erx＝0，
因为erx≠0，故有
由此可知，如果选择r为代数方程（5）的一个根，则erx就是方程（4）的一个特解.一般地，称
φ（r）＝r2＋pr＋q
为方程（4）的特征多项式.
方程（5）称为方程（4）的特征方程，特征方程的根称为特征根.于是，把求解微分方程（4）的问题归结为求代数方程（5）的根.
下面根据特征方程根的不同情况讨论方程（4）的通解.
①特征方程（5）有两相异实根r1和r2时，方程（4）有特解
又此两特解在（－∞，＋∞）内线性无关，故方程（4）的通解为
②特征方程（5）有两相等实根r1＝r2＝r时，只能得到方程（4）的一个特解y1＝erx，下面寻找另一个与之线性无关的方程（4）的特解y2，即y2为满足
≠常数的方程（4）的解.
设
＝u（x），即y＝u（x）y，把y代入（4）式，得212
约去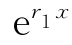
，并以u″、u′和u为准合并同类项得
u″＋（2r1＋p）u′＋（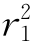
＋pr1＋q）u＝0.
注意 r1是特征方程（5）的二重根，故有r21＋pr1＋q＝0且2r1＋p＝0，于是得u″＝0.
为简便起见，不妨取u＝x，于是得y2＝xy1＝xerx与y1线性无关且为方程（4）的解.
因此，微分方程（4）的通解为
上述求y2的过程也可由前面介绍过的刘维尔公式直接写出（读者自行尝试）.
③特征方程（5）有一对共轭复根r1＝α＋βi，r2＝α－βi（β≠0）时，
方程（4）的两个特解也写为
，但它们是复值函数形式，为了得到实值函数形式，按如下步骤处理.
首先利用欧拉公式eiθ＝cosθ＋isinθ可将y1和y2改写为
由于复值函数y1和y2之间有共轭关系，可将它们相加除以2得实部，再相减除以2i得虚部，再利用方程（4）的解复合叠加原理，故实值函数
还是微分方程（4）的解，且
＝cotβx非常数，所以此时微分方程（4）的通解为
y＝eαx（C1cosβx＋C2sinβx）.
综上所述，求二阶常系数齐次线性方程y″＋py′＋qy＝0的步骤如下.
（1）写出方程（4）对应的特征方程r2＋pr＋q＝0.
（2）求特征方程对应的两个特征根r1和r2.
（3）由特征根的不同情形写出通解：
①当r1和r2为相异实根时，方程（4）的通解为y＝
②当r1＝r2时，方程（4）通解为y＝
③当r＝α±iβ时，方程（4）通解为y＝eαx（C1cosβx＋C2sinβx）（其中C1和C2为任意常数）.
例3 求下列二阶线性微分方程的通解.
（1）y″－3y′＋2y＝0； （2）y″＋4y′＋4y＝0；
（3）y″＋a2 y＝0（a＞0，常数）.
解 （1）对应齐次方程的特征方程为r2－3r＋2＝0，解得r1＝1，r2＝2.
故通解为y＝C1ex＋C2e2x，其中C1和C2为任意常数.
（2）对应齐次方程的特征方程为r2＋4r＋4＝0，解得r1＝r2＝－2.
故通解为y＝C1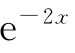
＋C2x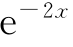
，其中C1和C2为任意常数.
（3）对应齐次方程的特征方程为r2＋a2＝0，解得r＝±ai.
故通解为y＝C1cos ax＋C2sin ax，其中C1和C2为任意常数.