二、介值定理
定理2 若函数f（x）在闭区间［a，b］上连续，且f（a）≠f（b），μ为f（a）与f（b）之间的任意一个数，则至少存在一点ξ∈（a，b），使得f（ξ）＝μ.
此定理的几何意义是，连续曲线y＝f（x）与水平直线y＝μ在开区间（a，b）上至少有一个交点（见图1－23）.
推论2 闭区间［a，b］上的连续函数可取得介于最大值M和最小值m之间的任何值.
证 设f（x）在闭区间［a，b］上连续，由最大值、最小值定理知：必存在x1，x2∈［a，b］，使得
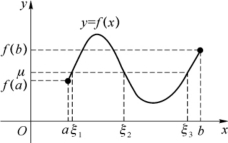
图1－23
任取μ∈［m，M］，由介值定理知：至少存在一点ξ介于x1和x2之间，使得
因为区间［x1，x2］和［x2，x1］都包含在［a，b］中，故而结论成立.
定理3（零点存在定理） 若函数f（x）在闭区间［a，b］上连续，且ff（a）f（b）＜0（即f（a）与f（b）异号），则在开区间（a，b）中至少存在一点ξ，使得f（ξ）＝0.
此定理的证明可由介值定理得到，因为0是f（a）与f（b）中间的值.
例1 证明x3－x－1＝0在（1，2）内至少有一个实根.
证 记f（x）＝x3－x－1，显然它在［1，2］上连续.又f（1）＝－1，f（2）＝5，两点处的值异号.由零点存在定理知，在（1，2）内至少有一个实数ξ，使得f（ξ）＝0，即方程x3－x－1＝0在（1，2）内有至少一个实根.
例2 证明实系数奇次代数方程至少有一个实根.
证 令f（x）＝a0xn＋
＋…＋
＋an（a0≠0），n为奇数.显然f（x）在（－∞，＋∞）上连续.不妨设a0＞0，则有
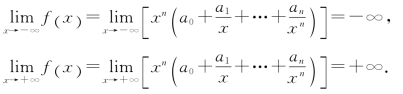
根据极限的保号性及函数的连续性，存在点x1，x2∈（－∞，＋∞），x1＜x2，使得f （x1）＜0，f （x2）＞0；由零点存在定理知，∃ξ∈［x1，x2］，使得f（ξ）＝0.
因此，方程a0xn＋
＋…＋
＋an＝0至少有一个实根.