习题6－6

习题6－6

1.验证下列函数组在其定义区间内线性相关性.

2.已知y1＝x2，y2＝x＋x2，y3＝ex＋x2都是方程（x－1）y″－xy′＋y＝－x2＋2x－2的解，求此方程的通解.

3.已知分别是方程y″－y′－2y＝x与y″－y′－2y＝ex的解，求方程y″－y′－2y＝x＋ex的通解.

4.验证y＝C1x5＋ln x（C1，C2为任意常数）是方程x2y″－3xy′－5y＝x2ln x的通解.

5.验证y＝C1ex＋C2e－x＋C3cos x＋C4sin x－x2（C1，C2，C3，C4为任意常数）是方程y（4）－y＝x2的通解.

＊6.已知y1（x）＝ex是齐次线性方程（2x－1）y″－（2x＋1）y′＋2y＝0的一个解，求此方程的通解.

＊7.已知y1（x）＝ex是齐次线性方程y″－3y′＋2y＝0的一个解，求y″－3y′＋2y＝ex的通解.

8.设y1（x），y2（x）是微分方程，y″＋p（x）y′＋q（x）y＝0的两个解，其中p（x），q（x）是连续函数，试证：y1y′2－y′1y2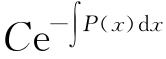＝（其中C为任意常数）.

9.对于齐次线性微分方程（A）：y″＋p（x）y′＋q（x）y＝0，其中p（x），q（x）是连续函数.

（1）证明：若1＋p（x）＋q（x）＝0，则y＝ex是方程（A）一个特解；

（2）证明：若p（x）＋xq（x）＝0，则y＝x是方程（A）一个特解；

（3）求方程（x－1）y″－xy′＋y＝0满足初值条件y（0）＝2，y′（0）＝1的特解.