总习题五
1.原式＝
2.被积函数为以π为周期的周期函数，故
由于sin22xtan x为奇函数，即
sin 2xtanxdx＝0，
故原式＝
3.利用分部积分法可得
所以f（0）＝3.
4.令t＝
5.
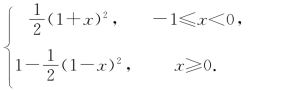
6.设F（x）＝
f（t）dt，G（x）＝
f（t）dt，x∈［a，b］，将F（x），G（x）在x＝
展成泰勒公式：
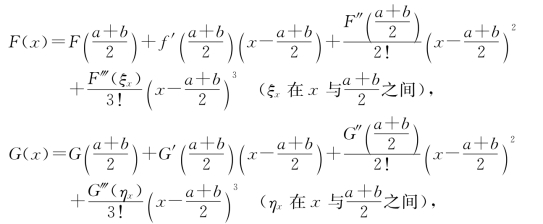
将x＝a代入F（x），求出F（a），将x＝b代入G（x），求出G（a），又G（a）＝G（b）＝0，从而有
利用介值定理存在ξ，使f″（ξ）＝
（f″（ξ）＋f″（η））代入上式即可.11
7.
8.
9.用分部积分法先求f（x）：
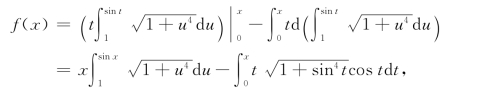
先求f′（x），再求f″（x）＝
10.a＝1；b＝0；c＝
11.C.
12.C.
13.设f（x）＝
，则f′（x）＜0，f（x）单调递减，从而在［n，n＋1］上有
利用迫敛性可求得原式＝0.
14.（1）f′（x）＝f（x）＋
≥2；
（2）F（a）＝－
＜0， F（b）＝
f（t）dt＞0，
又由（1）知F（x）严格递增，利用介值定理只有一个根.
15.将f（x）在x＝
展为一阶泰勒公式，由f″（x）＞0有f（x）＞f
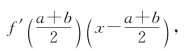
两端积分可得
16.
只有c＝1时极限存在且为ln＝2.
17.a＝b＝2（e－1）.
18.设In＝
（ln x）ndx，应用分部积分法得
19.设切点为（t，
），则切线方程为
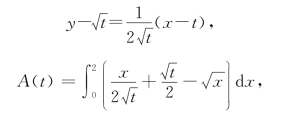
t＝1即（1，1）点处切线为所求
20.旋转体的体积为
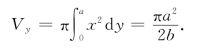
由Γ与y＝x＋1相切，在切点（x0，y0）处切线的斜率相同，可求得b＝
，代入V，y有Vy＝2π（a2－a3），可求得极大点a＝
，此时b＝
21.4.
22.（1）xf（x2）； （2）0； （3）x－1； （4）
（ea2－1）； （5）
（e－2）；
提示：原式＝
（利用分部积分法）＝
（设x－1＝t） ＝－
（6）0.
23.解：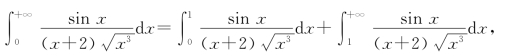
收敛.
又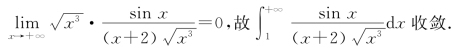
从而原积分收敛.
24.解：f（x）＝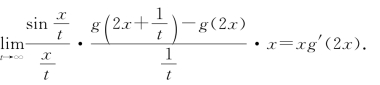
故
25.解：由
＝A，知f（0）＝0，f′（0）＝A，φ（0）＝0.
又φ（x）＝
f（xt）dt，设u＝xt，可得：
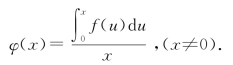
则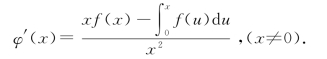
由导数定义，φ′（0）＝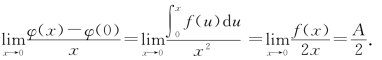
又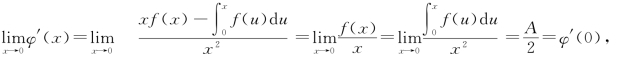
故g′（x）在x＝0连续.
26.解：（1）设F（x）＝
f（t）dt＋
f（t）dt，对F（x）在［0，x］上应用拉格朗日中值实理，存在θ∈（0，1），
使得F（x）－F（0）＝xF′（θx），
即
（2）对上式两边同除以x2，令x —→0＋取极限
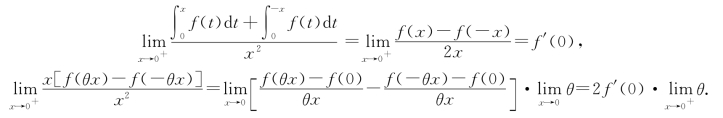
故由二者相等可得