第九节 欧拉方程
欧拉方程是一类特殊的线性微分方程，在工程实践中会经常用到.下面通过适当的变换可将其化为常系数线性微分方程来求解.形如
的微分方程称为欧拉方程，其中p1，p2，…，pn是常数.
这种方程的特点是各项变系数x的幂次与未知函数的求导阶数相同.
下面以二阶欧拉方程为例讨论这类方程解法.
作变换x＝et即t＝ln x（这里仅考虑x＞0情形，当x＜0时，作x＝－et变换即可）.借助于复合函数求导法则及
＝et＝x可得
即
代入方程（2），则
是一个以t为自变量的常系数线性微分方程.求出该方程的解，设为y＝y（t），于是y＝y（ln x）为方程（2）的解.
如果采用记号D表示对t求导的运算
，那么可得
xy′＝Dy， x2 y″＝（D2－D）y＝D（D－1）y.
继续运算可得出xky（k）＝D（D－1）…（D－k＋1）y，可代回原方程把更高阶欧拉方程化为常系数线性微分方程，从而可解.
例1 求出方程x2 y″＋xy′－y＝3x2的通解.
解 令x＝et，有t＝ln x，由式（3）可得原方程化为
对应齐次方程通解为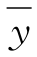
＝C1et＋C2e－t.
设非齐次方程特解为y＊＝ae2t，代入方程可得a＝1，因而y＊＝e2t.
于是，原方程的通解为y＝C1et＋C2e－t＋e2t，即
其中C1和C2为任意常数.
例2 求微分方程x2 y‴＋3xy″＋y′－
＝x满足初始条件y（1）＝
，y′（1）＝y″（1）＝
的特解.
解 原方程可变形为x3 y‴＋3x2 y″＋xy′－y＝x2，是欧拉方程.
设x＝et，得
D（D－1）（D－2）y＋3D（D－1）y＋Dy－y＝e2t，
整理得
D3 y－y＝e2t，
即
特征方程r3－1＝0解得r1＝1，r2，3＝－
，故齐次方程通解为
又2不是特征根，于是特解可设为y＊＝Ae2t，代入原方程，得A＝
，故y＊＝
故原方程通解为
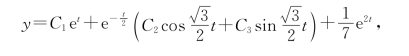
即
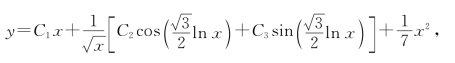
代入初始条件得，C1＝
，C2＝
，C＝0，从而所求特解为3
