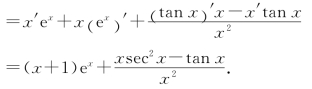导数的四则运算

一、导数的四则运算

设函数u（x），v（x）在点x处可导，则有

（1）［u（x）±v（x）］′＝u′（x）±v′（x）.

（2）［u（x）v（x）］′＝u′（x）v（x）＋u（x）v′（x）；

特别地，当u（x）＝C时，［Cv（x）］′＝Cv′（x），C为常数.

（3），v（x）≠0；

特别地，当u（x）≡1时，

上述运算通常称为导数的四则运算法则.

证

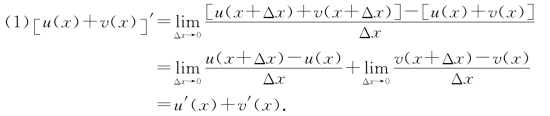
同理可证：［u（x）－v（x）］′＝u′（x）－v′（x）.

（2）

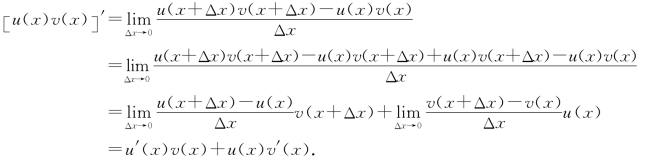
（3）

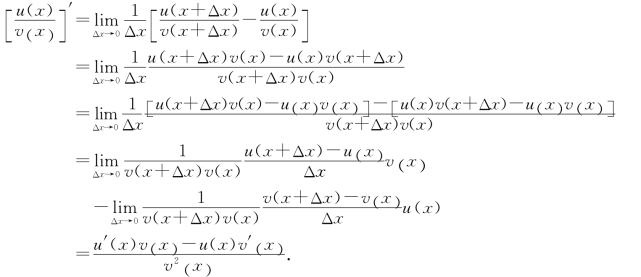
上述的证明过程应用了极限运算法则及v（x）在点x处的连续性〔因为v（x）在点x处可导〕.

导数四则运算法则中的（1）、（2）可推广到任意有限个可导函数的情形，即若u（x），v（x），ω（x）在点x处可导，则

［u（x）＋v（x）＋ω（x）］′＝u′（x）＋v′（x）＋ω′（x），

［u（x）v（x）w （x）］′＝u′（x）v（x）w （x）＋u（x）v′（x）w （x ）＋w′（x ）u （x ）v （x）.

例1 设y＝7＋2x＋3，求y′.

解 y′＝（7）′＋（2x）′＋3′＝7）′＋2xln 2＋0＝＋2xln 2.

例2 设y＝x2sin x，求y′

解 y′＝（x2）′sin x＋x2 （sinx）′＝2xsin x＋x2cos x，则

例3 设y＝tan x，求y′.

解

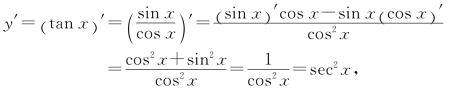
即

（tanx）′＝sec2 x.

用同样方法可得

（cotx）′＝－csc2 x.

例4 设y＝sec x，求y′.

解 y′＝＝sec xtan x，即

（secx）′＝sec xtan x.

同理可得：（cscx）′＝－csc xcot x.

例5 设y＝xex＋，求y′.

解 y′＝（xex ）′＋