微积分基本定理与基本公式
定义1 设f(x)在闭区间[a,b]上连续,从而对任何x∈[a,b],f(x)在[a,x]上可积.以积分上限x为自变量的函数
![]()
称为变上限积分.同样,可定义变下限积分
![]()
变上限积分与变下限积分统称为变限积分.
由于![]() =-
=-![]() ,因此以变上限积分为例讨论变限积分的性质.
,因此以变上限积分为例讨论变限积分的性质.
定理1 设f(x)在[a,b]上连续,则变上限积分
![]()
在区间[a,b]上处处可导,且
![]()
证 任取x∈[a,b],当增量Δx≠0(可正可负),且x+Δx∈[a,b]时,可利用积分中值定理,有
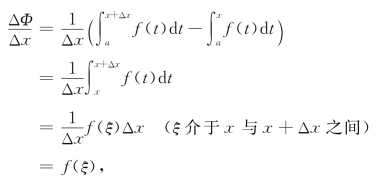
注意到当Δx→0时,ξ→x,以及f(x)在[a,b]上的连续性,有
![]()
由x的任意性,定理得证.
本定理证明了闭区间上的连续函数必有原函数,而且给出了一个定积分形式的原函数,从而称为原函数存在定理.由于它将不定积分与定积分联系起来,在微积分中有着非常重要的理论意义,又被誉为微积分学基本定理.
对于闭区间[a,b]上的连续函数f(x),由于变上限积分
![]()
为f(x)的一个原函数,因此f(x)的任一原函数F(x)必为
![]()
在此式中,令x=a,则C=F(a),从而有
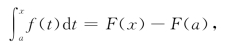
再令x=b,则有
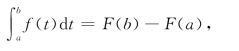
这便证明了下面的定理.
定理2 如果函数F(x)为连续函数f(x)在区间[a,b]上的一个原函数,则
![]()
式(1)称为牛顿-莱布尼茨公式.它表明一个连续函数在闭区间上的定积分等于它的任一原函数在此区间上的增量,从而把定积分的计算由求一个复杂和式的极限问题转化为求原函数的问题,这就给定积分的计算提供了一个简便而有效的方法,并在理论上又将定积分与不定积分联系起来.因此,式(1)又称为微积分学基本公式.为方便起见,式(1)常写成
![]()
例1 利用牛顿-莱尼茨公式计算下列积分:

解 (1)![]()
(2)![]()
(3)先求f(x)=![]() 的原函数,即不定积分
的原函数,即不定积分
![]()
取一个原函数F(x)=ln|ln x|,从而有
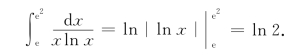
(4)先求被积函数的原函数.设![]() =t,则x=t2且dx=2tdt,从而有
=t,则x=t2且dx=2tdt,从而有
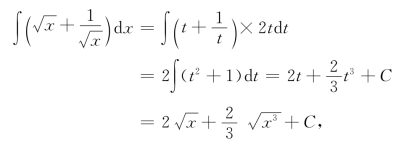
因此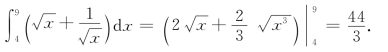
例2 求![]() ,其中
,其中
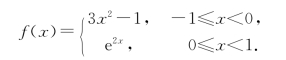
解 f(x)为分段函数,利用积分区间的可加性,有
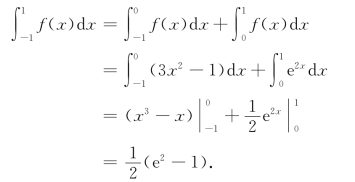
在上述解法中,![]() f(x)dx=
f(x)dx=![]() (3x2-1)dx意味着被积函数f(x)在x=0时函数值为-1,而实际上为1.在分段函数求定积分时经常遇到类似的情况.事实上,闭区间上的可积函数在改变其任何有限个点的函数值时,可积性和积分值不变.
(3x2-1)dx意味着被积函数f(x)在x=0时函数值为-1,而实际上为1.在分段函数求定积分时经常遇到类似的情况.事实上,闭区间上的可积函数在改变其任何有限个点的函数值时,可积性和积分值不变.
例3 求极限:

解 (1)设ψ(u)=![]() sintdt,u=x2.因此
sintdt,u=x2.因此![]() sintdt为复合函数,又因为分式为
sintdt为复合函数,又因为分式为![]() 型,利用洛必达法则和复合函数求导法,有
型,利用洛必达法则和复合函数求导法,有
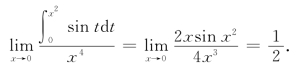
(2)将分子![]() (et-1)dt利用积分区间的可加性写为
(et-1)dt利用积分区间的可加性写为
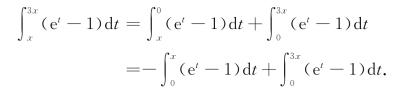
利用洛必达法则,并注意到等价无穷小替换,有
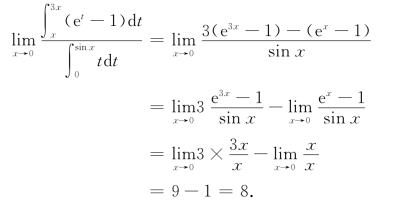
例4 设f(x)在[0,+∞)上连续,且在[0,+∞)上定义如下函数:
![]()
证明g(y)=h(y),y∈[0,+∞).
证 函数h(y)的被积函数与积分上限均含有自变量y,因而需化为变限积分,即
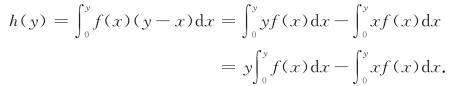
由于f(x)在[0,+∞)上为连续函数,由微积分基本定理知变限积分![]() f(t)dt处处可导,则也为连续函数,从而g(y),h(y)均处处可导,且有
f(t)dt处处可导,则也为连续函数,从而g(y),h(y)均处处可导,且有
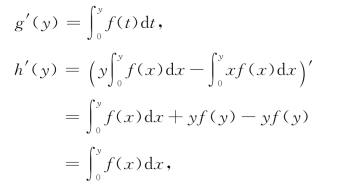
则对于任何y∈[0,+∞),有
g′(y)=h′(y),
因而,g(y)与h(y)相差一个常数.设
g(y)=h(y)+C,
由于g(0)=h(0),知C=0.这便证明了
g(y)=h(y), y∈[0,+∞).
例5 求极限:
(1)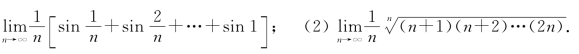
解 (1)由于f(x)=sin x在[0,1]上连续,从而可积.
将[0,1]等分为n份,分割细度λ=![]() ,取介点集{ξ}为每个小区间的右端点,则积分i和为
,取介点集{ξ}为每个小区间的右端点,则积分i和为
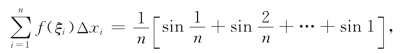
从而有
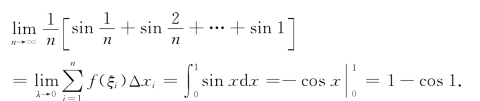
(2)设an=![]() ,则
,则
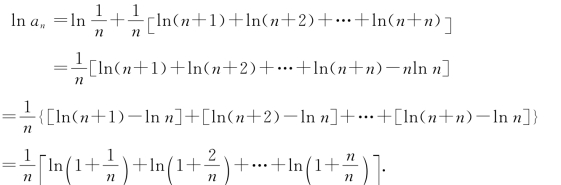
由于f(x)=ln(1+x)在区间[0,1]上连续,从而可积.将[0,1]区间n等分,且取介点集{ξi}为每个小区间右端点,则积分和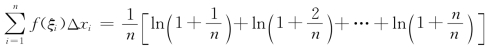 ,从而有
,从而有
![]()
由分部积分法可求ln(1+x)的原函数,为
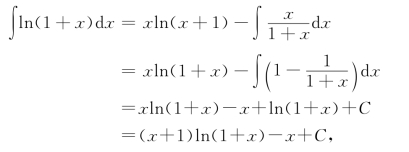
则
![]()
所以
![]()
