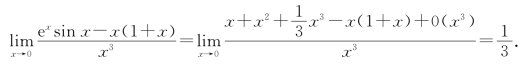带有佩亚诺型余项的泰勒公式
定理1 若函数f（x）在点x0存在直至n阶导数，则有
即
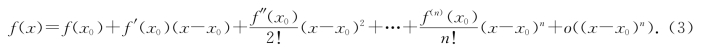
证 设Rn（x）＝f（x）－Tn（x）， Qn（x）＝（x－x0）n，只需证明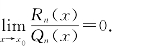
由关系式（2）可知，
并易知
由于f（ｎ）（x0）存在，则ｆ（x）在x0的某邻域u（x0）内存在直至n－1阶导函数.于是当ｘ∈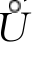
（x0）时（不妨设x＞x0），利用柯西中值定理n－1次，存在
ξ1∈（x0，x），ξ2∈（0，ξ1），…，ξn－2∈（0，ξn－3），ξ∈（0，ξn－2）
使得
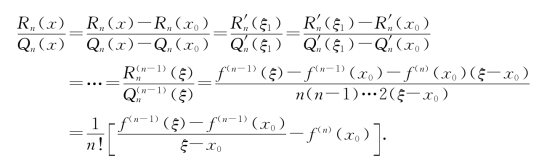
注意到当x→x0时，ξ→x0，从而有
式（3）称为函数f（x）在点x0处的泰勒公式，其中Rn（x）＝f（x）－Tn（x）称为泰勒公式的余项，形如o（（x－x0）n）型的余项称为佩亚诺型余项.所以式（3）又称为带有佩亚诺型余项的泰勒公式.
在学习导数和微分概念时已知，如果函数f（x）在点x0处可导，则有
f（x）＝f（x0）＋f′（x0）（x－x0）＋o（x－x0），
这实际上是n＝1时泰勒公式的特殊情形.
以后用得较多的是泰勒公式（3）在x0＝0时的特殊形式
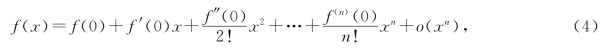
它也称为（带佩亚诺型余项的）麦克劳林（Maclaurin）公式.
另外，还需指出的是，若f（x）满足定理条件，n次多项式Pn（x）与f（x）满足
f（x）＝Pn（x）＋o（（x－x0）n），
可简单验证Pn（x）一定为泰勒多项式.这也就是说，在定理条件下，f（x）的n次逼近多项式是唯一的.这就为以后间接求一个函数的泰勒公式提供了理论依据.
例1 验证下列函数的麦克劳林公式.
（1）ex＝1＋x＋
＋o（xn）；
（2）sin x＝x－
＋…＋（－1）m－1
＋o（x2 m）；
（3）cos x＝1－
＋…＋（－1）m
＋o（x2 m＋1）；
（4）ln（1＋x）＝x－
＋…＋（－1）n－1
＋o（xn）；
（5）（1＋x）α＝1＋αx＋
（6）
＝1＋x＋x2＋…＋xn＋o（xn）.
证 这里只验证前两个公式，其余由读者自行证明.
（1）设f（x）＝ex.
因为
f（x）＝f′（x）＝…＝f（n）（x）＝ex，
所以
f（0）＝f′（0）＝…＝f（n）（0）＝1，
将这些值代入式（4），便得到ex的麦克劳林公式.
（2）设f（x）＝sin x.
由于f（k）（x）＝sin （x＋
），因此
f（2k）（0）＝0，f（2k－1）（0）＝（－1）k－1，k＝1，2，…，n，
将其代入式（4）.便得到sin x的麦克劳林公式.需要说明的是由于此时T2 m－1（x）＝T2 m（x），因此公式中的余项可写作o（x2 m－1），也可写作o（x2 m）.
以上公式在后续的学习中非常重要，务必熟记，利用这些公式可间接求得其他一些函数的麦克劳林公式，还可以用来求某种类型的极限.
例2 求f（x）＝ln x在x＝2处的泰勒公式.
解 由于ln x＝ln［2＋（x－2）］＝ln 2＋ln （1＋
）.
因此，利用例1中的麦克劳林公式（4），有
例3 写出f（x）＝
的麦克劳林公式，并求f（98）（0）与f（99）（0）.
解 用－
替换例1公式（1）中的x，便有
为所示的麦克劳林公式（由n次逼近多次式的唯一性）.
由泰勒公式分数的定义，在上述f（x）的麦克劳林公式中，x98与x99的系数分别为
由此可知，f（98）（0）＝－
，f（99）（0）＝0.
例4 求极限
解 本题分子涉及例1中的函数，且分母为多项式函数，故考虑将分子用麦克劳林公式表示（写到3次项）：
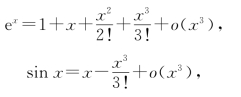
因而
