三、柯西（Cauchy）审敛原理
极限存在准则给出了数列收敛的充分条件，柯西审敛原理将给出数列收敛的充分必要条件.
定理1 数列｛xn｝收敛的充分必要条件是：对∀ε＞0，∃N，当m，n＞N时，有
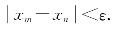
证 必要性.设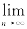
xn＝a，则对∀ε＞0，∃N，当m，n＞N时，有
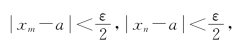
此时
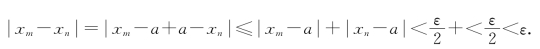
充分性的证明需要更多的知识，在此略去.
柯西审敛原理的几何意义是：对∀ε＞0，总可以找到自然数N，当数列的项数n大于N时，其任意两项的差都小于给定的数ε.
柯西审敛原理不仅有很大的理论价值，也可用于判断某些级数的敛散性（见第十章）.
例9 设xn＝1＋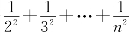
，证明数列｛x｝收敛.n
证 对∀ε＞0，不妨设m＞n，有
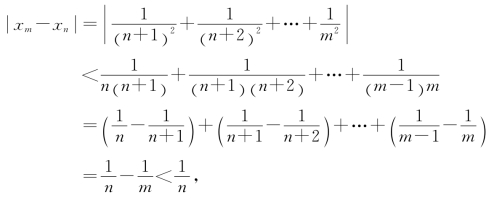
要使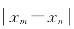
＜ε，只要取n＞
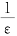即可.所以，对∀ε＞0，∃N＝
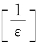，当m，n＞N时，有
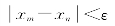
恒成立.由柯西审敛原理知，数列x｛｝n收敛.
