不定积分的性质

三、不定积分的性质

定理2 设f（x）与g（x）在区间I上均存在原函数，λ，μ为任意实数，则λf（x）＋μg（x）也在区间I上存在原函数，且

证 由于

按照求导法则，有

从而有

特别地，此定理中当λ＝μ＝1时，有

当μ＝0时，有

此运算性质称为线性法则，可证明其一般形式

利用基本积分公式和以上运算法则可求一些简单的积分.

例1 求不定积分：

（1）∫（a0xn＋a1xn－1＋…＋an－1x＋an）dx；　　（2）∫（5x＋5－x）2dx；

（3）∫dx；　　　　　　　　　　　（4）∫（sin x＋＋ex ）dx.

解 （1）原式＝＋anx＋C.

（2）原式＝∫［25x＋2＋（x）］dx

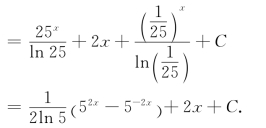
（3）原式＝∫＝∫（csc2 x＋sec2x ）dx＝－cot x＋tan x＋C.

（4）原式＝－cos x＋2arctan x＋ex＋C.

例2 已知曲线在x点的切线的斜率为x，且经过点（2，），求此曲线方程.

解 设曲线方程为y＝f（x）.

由已知条件f′（x）＝x.

所以

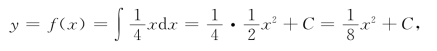
将x＝2，y＝代入上式，求得C＝2.

故所求曲线为y＝x2＋2.