函数组的线性相关性

二、函数组的线性相关性

定义1 设有一组不全为零的常数k1，…，kn，使对任意x∈D（D为某区间）恒有

称函数组y1（x），y2（x），…，yn（x）在区间D上线性相关；否则，当且仅当k1＝k2＝…＝kn＝0时式（3）才成立，称函数组y1（x），y2（x），…，yn（x）在D上线性无关.

例1 求证函数组cos 2x，sin 2x在（－∞，＋∞）内线性无关.

证 （方法一）设有实数k1和k2，对任意x∈（－∞，＋∞）有

k1cos 2x＋k2sin 2x≡0.

取特殊值x＝0及x＝，代入方程，得

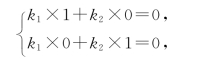
因而k1＝k2＝0，于是函数组cos 2x，sin 2x在（－∞，＋∞）内线性无关.

（方法二）设有

k1cos 2x＋k2sin 2x≡0，

两边对x求导，得

－2k1sin 2x＋2k2cos 2x≡0.

系数行列式

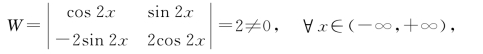
故k1＝k2＝0，说明所给函数组在（－∞，＋∞）内线性无关.

由方法二可得，一般而言，对n个函数y1，y2，…，yn，若行列式

则函数组y1，y1，…，yn在D上线性无关.

例2 求证函数组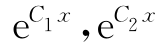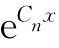，…（其中，C1，…，Cn为互不相等的常数）线性无关.

证 W＝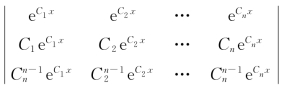

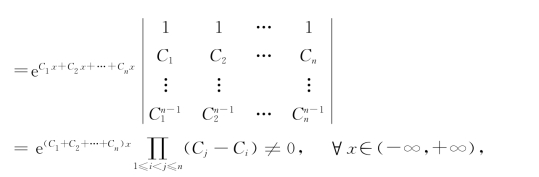
故该函数组y1，y2，…，yn在（－∞，＋∞）上线性无关.

值得关注的是，对于任意两个函数，它们线性相关与否，由定义，只要看它们的比是否为常数：如果比为常数，那么它们就线性相关；否则就线性无关.