自变量趋于无穷大时函数的极限

二、自变量趋于无穷大时函数的极限

如果在自变量x→∞的过程中，对应的函数值f（x）无限接近于某确定的常数A，那么称A为函数f（x）当x→∞时的极限.精确定义如下：

定义3 设函数f（x）在大于某一正数时有定义.如果对∀ε＞0，∃X＞0，当＞X时，恒有

成立，则称常数A为函数f（x）当x→∞时的极限，记作

此外，可类似定义f（x）＝Af（x）＝A（由读者自行给出精确定义）.

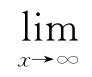f（x）＝A的几何意义：对于任意给定的ε＞0，总存在X＞0，当x＞X或x＜－X时，曲线y＝f（x）位于两直线y＝A＋ε与y＝A－ε之间（见图1－16）.

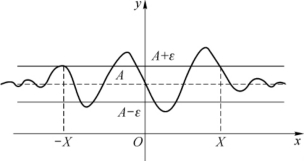
图1－16

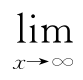f（x）＝A表示曲线y＝f（x）有水平渐近线y＝A.

函数极限的性质对x→∞，x→＋∞，x→－∞同样成立，不再一一赘述.

例6 证明ex＝0.

证 因为ε是任意小的正数，不妨设0＜ε＜1，要使得

成立，只需

x＜lnε，

所以，对于每一个0＜ε＜1，∃X＝－lnε＞0，当x＜－X时，有＜ε，即ex＝0.