二、函数的间断点

二、函数的间断点

定义4 若f（x）在点x0的某邻域内有下列三种情况之一：

（1）在点x0没有定义；

（2）在点x0有定义，但f（x）不存在；

（3）在点x0有定义，且f（x）存在，但f（x）≠f （x0）；

则称f（x）在点x0不连续，点x0称为函数f（x）的不连续点或间断点.

为方便起见，把f（x）的间断点分为两类：

（1）若f（x）在点x0的左、右极限都存在，但f（x）在点x0不连续，则称x0为f（x）的第一类间断点.需特别指出的是，若此时f（x）存在，称x0为f（x）的可去间断点；若此时不存在，称x0为f（x）的跳跃间断点.如在例2中，f（x）在x＝1的左、右极限都存在但不相等，即不存在，故x＝1是f（x）的跳跃间断点.

（2）若x0是f（x）的间断点，但不是第一类间断点，称x0为f（x）的第二类间断点.

例4 讨论函数f（x）＝在x＝0的连续性.

解 函数在x＝0无定义，所以x＝0是函数f（x）的间断点.根据重要极限知，f（x）＝＝1.

函数f（x）在x＝0处极限存在，所以x＝0是f（x）的第一类可去间断点.

事实上，补充定义函数在x＝0的值，形成一新函数，即

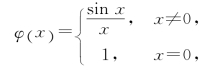
此时，φ（x）在点x＝0连续.

例5 讨论y＝在x＝0的连续性.

解 函数在x＝0无定义，所以x＝0是函数的间断点.当x→0时，的函数值在

－1与＋1之间无穷次振荡（见图1－14），所以不存在.因此x＝0是函数的第二类间断点.

例6 讨论函数y＝在x＝0的连续性.

解 函数y＝在点x＝0无定义.又＝＋∞，＝0，即函数在x＝0的右极限不存在，因此x＝0是函数的第二类间断点.