＊三、相关变化率

导数就是因变量对自变量的变化率.在参数方程x＝φ（t），y＝ψ（t）中，x和y因参数t而存在函数关系，因此它们的变化率也存在一定的关系，这两个变化率相互关联，称作相关变化率.于是，若已知其中一个变量在某一时刻的变化率，就可以求出另一变量在同一时刻的变化率.

例10 有一长度为5m的梯子靠在铅直的墙上，如果梯子下端沿地板以3m／s的速度离开墙根滑动，问当梯子下端距墙根1.4m时，梯子的上端下滑的速度是多少？

解 设梯子下端距墙根的距离为x＝x（t）m，梯子上端距墙根的距离为y＝y（t）m（如图2－3所示）.由题意知，y和x存在函数关系

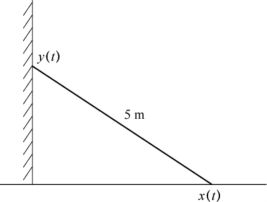
图2－3

两边对t求导，得

又已知＝3，当x＝1.4m时，

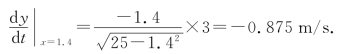
y对时间t的变化率是负值，指梯子上端下滑的速度为0.875m／s.