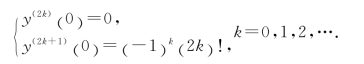第三节 高阶导数
对于y＝f（x）的导函数f′（x），它仍然是x的函数，可以继续讨论它的可导性.若f′（x）对x仍可导，则称其导函数为y＝f（x）的二阶导数，记作
即
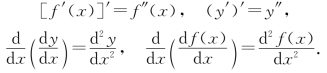
若用定义表示y＝f（x）在x0的二阶导数，则有
或
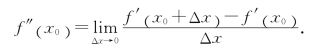
如果对f″（x）关于x再求导，如果导数存在，称这个导数为y＝f（x）的三阶导数，记作
一般而言，y＝f（x）的n阶导数为
也记作
二阶或二阶以上的导数统称为高阶导数.由于初等函数的导函数仍为初等函数，所以求高阶导数就是反复利用前面所讲的求导法则和求导公式.
若函数f（x）在区间（a，b）内存在n阶导数，且f（n）（x）在（a，b）内连续，则记为f（x）∈C（n）（a，b）.
下面说明二阶导数的物理意义.已知变速直线运动物体的位移函数s＝s（t），则t时刻的瞬时速度v（t）＝
，即位移对时间t的变化率；又由运动学知，此时运动的瞬时加速度应为瞬时速度v（t）对时间t的变化率，即
也就是说瞬时加速度为位移函数s（t）的二阶导数.
例1 设y＝
，求y″，y‴.
解 因y′＝
，则
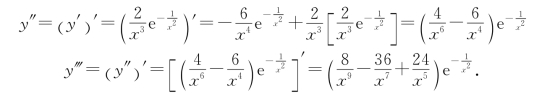
例2 求n次多项式Pn（x）＝a0xn＋a1xn－1＋…＋an的各阶导数.
解 易知P′n（x）＝na0xn－1＋（n－1）a1xn－2＋…＋an－1，
P″n（x）＝［P′n（x）］′＝n（n－1）a0xn－2＋（n－1）（n－2）a1xn－3＋…＋2an－2.
每求一次导数，多项式的次数就降低一次，因此可知，Pn（x）的k阶导数为：
（1）k≤n时
Pn（k）（x）＝n（n－1）…（n－k＋1）a0xn－k＋（n－1）（n－2）…（n－k）a1xn－k－1＋…＋（k－1）！an－k＋1x＋k！an－k.
（2）k≥n＋1时
Pn（k）（x）≡0，
特别地
例3 设y＝sin x，求y（n）.
解 反复利用三角函数的恒等式cos x＝
有
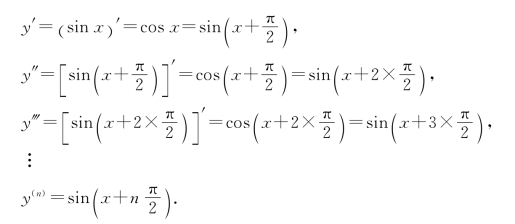
一般而言，用数学归纳法可以证明如下常见函数的高阶导数公式：
（1）（xn）（n）＝n！；
（2）（ax）（n）＝（ln a）nax，（ex）（n）＝ex；
（3）（sinx）（n）＝sin （x＋n
）；
（4）（cosx）（n）＝cos （x＋n
）；
（5）［（1＋x）α］（n）＝α（α－1）…（α－n＋1 ）（1＋x）α－n.
求函数的高阶导数有下列运算法则.
设u＝u（x），v＝v（x）皆n阶可导，则如下的四则运算法则成立：
（1）［u（x）±v（x）］（n）＝u（n）（x）±v（n）（x）；
（2）［Cu（x）］（n）＝Cu（n）（x），C为常数；
（3）莱布尼茨（Leibniz）公式
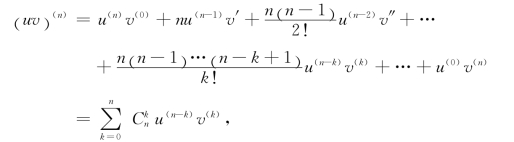
其中u（0）＝u，v（0）＝v.
只证明（3），用数学归纳法证明如下：
当n＝1时，（uv）′＝u′v（0）＋u（0）v′＝u′v＋uv′.
设当n＝k时公式成立，即
则当n＝k＋1时，对上式关于x再求导一次，于是有
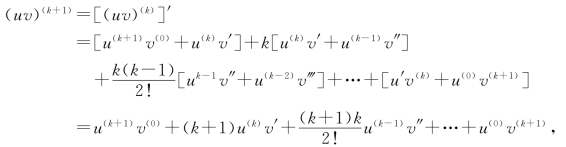
因此高阶求导公式对任何自然数n成立.
例4 设y＝x2sin x，求y（100）.
解 取u＝sin x，v＝x2，则
v′＝2x，v″＝2，v（n）≡0（当n≥3时）.
由莱布尼茨公式得
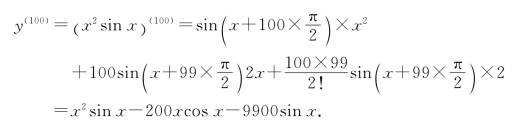
例5 设y＝arctan x，求y（n）（0）.
解 y（0）（0）＝y（0）＝0.
由y′＝
知（1＋x2 ）y′＝1，且
y′（0）＝1.
又y″＝
，得
y″（0）＝0.
现对等式（1＋x2 ）y′＝1两边同时求n阶导数，由莱布尼茨公式，则当n＞1时
即
令x＝0，有
y（n＋1）（0）＝－n （n－1 ）y（n－1）（0），
于是递归得到
