四、初等函数
1.基本初等函数
在初等数学中，常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数统称为基本初等函数.它们分别是：
（1）常数函数y＝C，D＝（－∞，＋∞）；
（2）幂函数y＝xα，α是常数，D＝（0，＋∞）；
（3）指数函数y＝ax，a＞0，a≠1，D＝（－∞，＋∞），（a＝e时，y＝ex）；
（4）对数函数y＝logax，a＞0，a≠1，D＝（0，＋∞），（a＝e时，y＝ln x）；
（5）三角函数
正弦函数y＝sin x，D＝（－∞，＋∞），
余弦函数y＝cos x，D＝（－∞，＋∞），
正切函数y＝tan x，D＝
余切函数y＝cot x，D＝
正割函数y＝sec x，D＝
余割函数y＝csc x，D＝
（6）反三角函数
反正弦函数y＝arcsin x，D＝［－1，1］，
反余弦函数y＝arccos x，D＝［－1，1］，
反正切函数y＝arctan x，D＝（－∞，＋∞），
反余切函数y＝arccot x，D＝（－∞，＋∞）.
2.初等函数
初等函数指由基本初等函数经过有限次的四则运算和有限次复合运算而产生并可用一个数学式表达的函数.
例如，y＝ln tan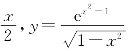
，…都是初等函数.分段表示函数一般不是初等函数.例如，y＝sgn x，y＝［x］都不是初等函数.
工程技术中经常要用到一类函数——双曲函数，它们是由指数函数y＝ex与y＝e－x生成的初等函数，定义如下：
双曲正弦函数sh x＝
，D＝（－∞，＋∞）（见图1－9（a））；
双曲余弦函数ch x＝
，D＝（－∞，＋∞）（见图1－9（b））；
双曲正切函数th x＝
，D＝（－∞，＋∞）（见图1－9（c））；
双曲余切函数cth x＝
，D＝（－∞，＋∞）（见图1－9（d））.
其中，sh x，th x，cth x是奇函数，ch x是偶函数.
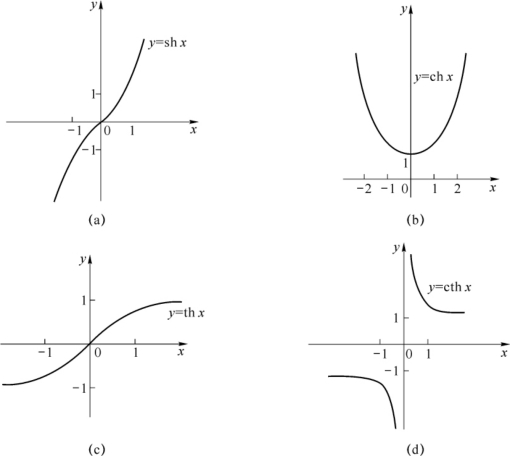
图1－9
类似于三角函数，双曲函数也具有恒等式，如
ch2 x－sh2 x＝1；
sh 2x＝2sh xch x；
ch 2x＝ch2 x＋sh2 x；
sh （x±y）＝sh xch y±ch xsh y；
ch （x±y）＝ch xch y±sh xsh y.
双曲函数的反函数称为反双曲函数，它们分别为
反双曲正弦y＝arcsh x＝ln （x＋
），D＝（－∞，＋∞）；
反双曲余弦y＝arcch x＝ln （x＋
），D＝［1，＋∞）；
反双曲正切y＝arcth x＝
，D＝（－1，1）.