三、一致连续性

三、一致连续性

本章第八节给出了函数f（x）在一点x0连续的定义，即对∀ε＞0，∃δ＞0，当｜x－x0｜＜δ时，

恒成立.

在此定义中，δ的选取与x0和ε有关，是否存在与点x0无关的选取方式呢？

定义1 设函数f（x）在区间I上有定义，如果对任意给定的ε＞0，总存在δ＞0，使得对区间I上的任意两点x1，x2，当｜x1－x2｜＜δ时，有

那么称f（x）在区间I上一致连续.

此定义表明：对于区间I上任意两点，当其距离小于δ时，对应的函数值的差的绝对值就小于给定的正数ε.此时δ显然只与ε有关，即δ＝δ（ε）.

由上述定义可知：若函数f（x）在区间I上一致连续，则它在区间I上连续，但反过来不一定成立.

例3 证明f（x）＝sin x在（－∞，＋∞）上一致连续.

证 对∀ε＞0，对于任意的x1，x2∈（－∞，＋∞），要使

只要

取δ（ε）＝ε，则当｜x1－x2｜＜δ时，有

所以f（x）＝sin x在（－∞，＋∞）上一致连续.

例4 证明f（x）＝在［a，1］（0＜a＜1）上一致连续而在（0，1］上连续但非一致连续.

证 对∀ε＞0，对于任意的x1，x2∈［a，1］，要使

只要

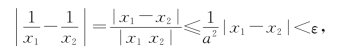
即

取δ＝a2ε，则当｜x1－x2｜＜δ时，有

即f（x）＝在［a，1］上一致连续，因而在［a，1］上连续.

对ε0＝＞0，取x1＝，x2＝∈（0，1），x1－x2＝可以任意小，但

即f（x）＝在（0，1）上非一致连续.

如何判断一个函数是否一致连续？有下面的定理：

定理4（一致连续性定理） 闭区间［a，b］上的连续函数f（x）一定在［a，b］上一致连续.

证略.