费马定理与罗尔定理
按照导数的几何意义，如果函数f（x）在x0处有水平切线，则意味着函数f（x）在x0点的导数f′（x0）＝0，这样的点x0称为函数的驻点（或稳定点）.函数的驻点在后续的学习中非常重要.本节将讨论的费马定理和罗尔定理分别告诉我们什么样的点必为驻点，什么样的函数必存在驻点.
设函数f（x）在x0的某邻域U（x0）内对一切x∈U（x0）有
f（x0）≥f（x） （f（x0）≤f（x）），
则称函数f（x）在x0取得极大（小）值，称x0为f（x）的极大（小）值点.极大值点和极小值点统称为函数的极值点.
由极值点的定义可知，若函数f（x）在x0取得极值，x0未必为函数的连续点（见图3－1），更未必为函数的可导点（见图3－2）.如果x0既是函数f（x）的极值点，又是可导点，则x0必为函数f（x）的驻点（见图3－3），这就是以下的费马定理.
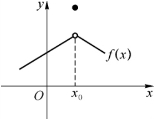
图3－1
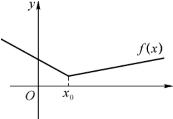
图3－2
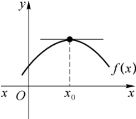
图3－3
费马定理 设函数f（x）在x0的某邻域U（x0）内有定义，在x0处取得极值，且f′（x0）存在，则f′（x0）＝0.
证 由于f′（x0）存在，也就是
f′＋（x0）＝f′－（x0）＝f′（x0）.
设x0为f（x）的极大值点，那么存在正数δ，使得对一切x∈（x0，x0＋δ）⊂U（x0），有
而对一切x∈（x0－δ，x0）⊂U（x0），有
由极限的性质可得
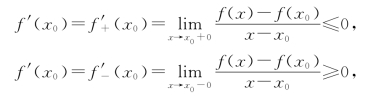
从而有
f′（x0）＝0.
罗尔定理 如果函数f（x）满足如下条件：
（1）在闭区间［a，b］上连续；
（2）在开区间（a，b）内可导；
（3）f（a）＝f（b）；
则在（a，b）内至少存在一点ξ，使得f′（ξ）＝0.
罗尔定理的几何意义是：在处处可导的一段曲线上，如果曲线两端点高度相等，则至少存在一条水平切线.
证 由于f（x）在闭区间［a，b］上连续，则必存在最大值M与最少值m.分以下两种情况讨论.
（1）M＝m.此时f（x）在［a，b］上为常数.ξ可取（a，b）内任何点，结论成立.
（2）M＞m.由于f（a）＝f（b），则M与m至少有一个不在端点处取得.不妨设M在开区间（a，b）内部取得，则至少存在一点ξ∈（a，b）使f（ξ）＝M.由极大值点的定义可知，ξ为f（x）在（a，b）内的极大值点.根据费马定理有f′（ξ）＝0.
注意 罗尔定理中三个条件缺少任何一个，结论不一定成立（见图3－4）.
例1 设
＋an＝0，其中a0，a1，…，an均为实数.求证方程a0xn＋a1xn－1＋…＋an－1x＋an＝0在（0，1）内至少存在一实根.
证 设f（x）＝
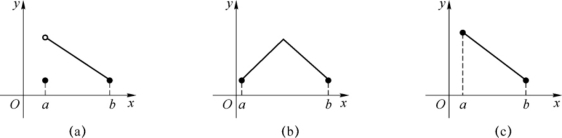
图3－4
则
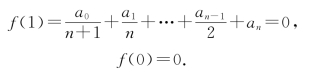
易验证f（x）在［0，1］上满足罗尔定理的条件，从而至少存在一点ξ∈（0，1），使f′（ξ）＝0，即f′（x）＝a0xn＋a1xn－1＋…＋an－1x＋an＝0在（0，1）内至少存在一实根.
例2 设f（x）在［a，b］上连续，在（a，b）内二阶可导，且f（a）＝f（c）＝f（b），c∈（a，b）.证明至少存在一点ξ∈（a，b），使f″（ξ）＝0.
证 分别在［a，c］和［c，b］上对f（x）利用罗尔定理，则存在ξ1∈（a，c），ξ2∈（c，b），使f′（ξ1）＝0，f′（ξ2）＝0.
再在［ξ1，ξ2］上对f′（x）利用罗尔定理，则至少存在一点ξ∈（ξ1，ξ2）⊂（a，b），使得f″（ξ）＝0.