可分离变量的微分方程
下面讨论微分方程的解法，首先介绍一阶微分方程常用的分离变量法、齐次方程解法、一阶线性微分方程解法及全微分方程解法（全微分后介绍），然后再介绍几种常见可降价的高阶方程解法，最后给出二阶线性常系数微分方程解法.
显式形式表示的一阶方程为
微分形式表示的一阶方程为
注意到（2）式中变量x与变量y对称，既可看作以x为自变量，y为未知函数方程，即
又可看作以y为自变量，x为未知函数的方程，即
如果方程（1）右端f（x，y）可以化为x的函数与y的函数相乘的形式，即
或方程（2）中P（x，y）和Q（x，y）可各自分解为x的函数与y的函数相乘的形式，即
整理得
则称方程（1）或方程（2）为可分离变量方程.
这种方程的解可以通过两端积分的方法得到.
假定方程（4）中的φ（x）和ψ（y）连续.设y＝f（x）是方程（4）的解，将它代入得恒等式
ψ［f（x）］f′（x）dx＝φ（x）dx
两端积分并由y＝f（x）引入变量y得
设Ψ（y）及Φ（x）分别为ψ（y）及φ（x）的原函数，于是有
故（4）式的解满足关系式（5）.
反之，若y＝f（x）是由（5）式所确定的隐函数，那么在ψ（y）≠0条件下，y＝f（x）也是方程（4）的解.事实上，由隐函数求导公式知，当ψ（y）≠0时
表明y＝f（x）满足关系式（4）.
所以，若已分离变量的方程（4）中φ（x）和ψ（y）连续，且ψ（y）≠0，那么方程（4）两端积分后所得关系式（5）就用隐式给出了方程（4）的解，称为隐式解，且为隐式通解（当φ（x）≠0时（5）式确定隐函数x＝g（y）也可认为是方程（4）的解）.
例1 求解方程
解 分离变量后得
两边积分，得
即
ln y＝ln x＋C1，
若记C1为ln C2，则有ln y＝ln C2x，于是
y＝C2x（C2为任意常数）
注意 事实上，在取不定积分时，知
＝ln｜y｜＋C，则上述过程严格的解法应为
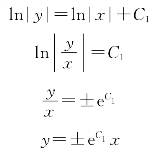
令±eC1＝C2为任意常数，又y＝0也是解，则得到相同形式的解
y＝C2x.
因为作为微分方程通解的常数C，并不需要详细讨论其范围，而只作为一种形式上常数出现.
例2 解方程（1＋y2）xdx＋（1＋x2）ydy＝0.
解 分离变量后得
两边积分得
化简，得
（1＋x2）（1＋y2）＝C，
其中C为任意常数.
例3 解方程
f（xy）.
解 原方程看似无法分离变量，但若令u＝xy，则
.代入原方程，整理可
得
分离变量，可得
两端积分，有
其中C为任意常数.
例4 生物种群生长的数学模型
1798年，英国人口学家马尔萨斯（Malthus）根据大量人口统计资料指出：假设没有人口的移入和迁出，那么人口增长率是与当时的人口数量成正比的.如果在t时刻的人口数量为P（t），t以年为单位，则其增长率为
式中k＞0为比例常数.
方程（6）是可分离变量的微分方程，其解为P＝P0ekt，P0是P的初始值.当k＞0时.P按指数规律增长；当k＜0时，P按指数规律衰减.因此，方程（6）也称为人口P的指数增长或指数衰减模型——马尔萨斯模型.
自然界中许多量的变化都与本身的大小成一定的比率，如细菌的繁殖、放射性物质的质量、按复利计算的投资收益等，这些问题都适用于指数增长模型.
马尔萨斯模型在描述人口增长问题上曾经是相当成功的.例如，1700—1961年，世界人口的相对增长率
大致为一个常数，故马尔萨斯模型很好地描述和预测了该时期的人口状况，但根据马尔萨斯模型，人口将按指数规率无限增长，显然也不切实际.
荷兰数学家弗胡斯特（Verhulst）考虑到“密度制约”因素，即种群生活在一定的环境中，在资源一定的情况下，人口数目越多，每个个体获得的资源就越少.提出了更能准确描述人口增长的模型——逻辑斯谛（Logistic）模型.
常数k，a可以根据相对增长率的历史数据测得.方程（7）可变形为
其中L＝
.当P＝L时，
＝0，可知L是人口的极值，表示环境所能承受的最大人口数量.
逻辑斯谛方程（8）的解为
其中常数C＝
可由初始条件P（0）＝P确定，即0
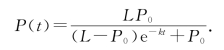
由上式，当t→＋∞时，P（t）→L，表明随时间增加，种群总数将逐渐稳定为常数.
研究人员用逻辑斯谛模型对美国人口作了预测，结果是1790—1940年的预测值与实际值都相当吻合.以我国1949—1957年的数据，预测我国1978—2000年的人口数量，结果也相当吻合.但是，逻辑斯谛模型无法准确地描述美国1950年后的人口情况，这说明没有一个模型是完备的.人们还可以继续寻找比逻辑斯谛模型更好的人口模型.