y″＝f（y，y′）型的微分方程

三、y″＝f（y，y′）型的微分方程

方程

的右端不显含自变量x.

为将二阶方程化为一阶方程，令y′＝q（y），则y″＝，代入原方程中则有

这是一个q关于自变量y的一阶微分方程，若其通解为q＝ψ（y，C1），即y′＝ψ（y，C1），原方程的通解为

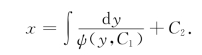
例5 解方程y″＋（y′）2＝0.

解 方程不显含自变量x，故可令y′＝q（y），于是y″＝q

原方程可化为

当q≠0时有

由分离变量法，可解得

q＝C1（y－1）2，

即

y′＝C1（y－1）2，

再用分离变量法，可得

其中C1，C2为任意常数.

某些特殊的高于二阶的微分方程也可用降阶法求解.

例6 求微分方程y‴＝2y″2满足初始条件y（0）＝y′（0）＝0，y″（0）＝1的特解.

解 令y″＝p（x），则y‴＝p′（x），原方程化为

p′＝2p2，

由分离变量法解得

把初始条件y″（0）＝p（0）＝1代入得C1＝－1，因此，y″＝p＝，两边积分，得

把初始条件y′（0）＝0代入得C2＝0，因此

再两端积分，得

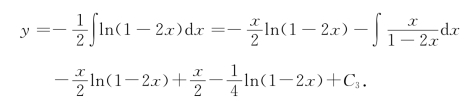
把初始条件y（0）＝0代入上式得C3＝0.

于是，所求特解为y＝－ln（1－2x）＋ln（1－2x）.