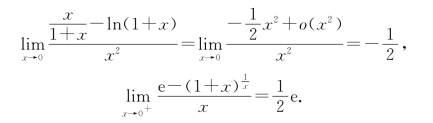型不定式的极限
2025年09月17日
一、
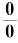 型不定式的极限
型不定式的极限
定理1 若函数f(x)和g(x)满足:
(1)![]() f(x)=
f(x)=![]() g(x)=0;
g(x)=0;
(2)在点x0的某去心邻域![]() (x0)内二者均可导,且g′(x)≠0;
(x0)内二者均可导,且g′(x)≠0;
(3)![]() =A(A可为实数,也可为±∞或∞);
=A(A可为实数,也可为±∞或∞);
则
![]()
证 补充定义f(x0)=g(x0)=0,这样f(x)与g(x)均在x0连续.任取x∈U(x0)(不妨设x>x0),在区间[x0,x]上应用柯西中值定理,存在ξ∈(x0,x),使
![]()
注意到x→x0时,也有ξ→x0,从而有
![]()
注意 将定理中的x→x0换成x→![]() ,x→
,x→![]() 也有同样的结论.若将x→x换成x→0±∞或x→∞(相应地修改条件(2)的邻域),只需利用变换x=
也有同样的结论.若将x→x换成x→0±∞或x→∞(相应地修改条件(2)的邻域),只需利用变换x=![]() ,也可得到同样的结论,证明过程由读者自行完成.
,也可得到同样的结论,证明过程由读者自行完成.
例1 求极限![]()
解 这是![]() 型不定式极限.设f(x)=1+cos x,g(x)=tan2 x.
型不定式极限.设f(x)=1+cos x,g(x)=tan2 x.
因为
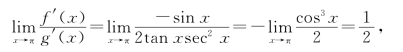
由洛必达法则知
![]()
例2 求极限![]()
解 这是![]() 型不定式极限,可利用两次洛必达法则计算如下:
型不定式极限,可利用两次洛必达法则计算如下:
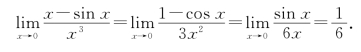
例3 求极限![]()
解 这是![]() 型不定式极限,可连用三次洛必达法则计算:
型不定式极限,可连用三次洛必达法则计算:
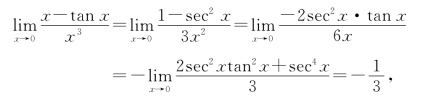
或利用一次洛必达法则计算:
![]()
洛必达法则有时与等价无穷小代换、重要极限、泰勒公式等重要求极限方法结合使用,效果会更好.
例4 求极限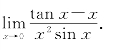
解 这是![]() 型不定式极限.如果直接利用洛必达法则分母的导数较烦琐.若用x代替其等价无穷小sin x就方便多了.
型不定式极限.如果直接利用洛必达法则分母的导数较烦琐.若用x代替其等价无穷小sin x就方便多了.
![]()
例5 计算极限![]()
解 这是![]() 型不定式极限.用洛必达法则得
型不定式极限.用洛必达法则得
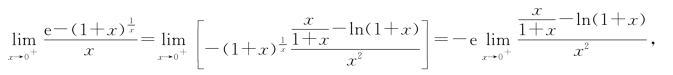
此时仍为![]() 型不定式极限,可继续利用洛必达法则计算(读者自行完成),下面用泰勒公式来
型不定式极限,可继续利用洛必达法则计算(读者自行完成),下面用泰勒公式来
计算.因
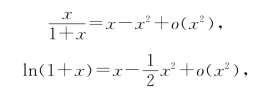
从而