函数的凸凹性与拐点
第四节通过导函数研究了可导函数的单调性.考察函数y＝x2与y＝
（见图3－9）在（0，＋∞）上的图像时可知，虽然二者均为严格增函数，但二者的弯曲方向不同，前者向上凹，而后者向上凸.这一节研究函数的这种凸凹性.
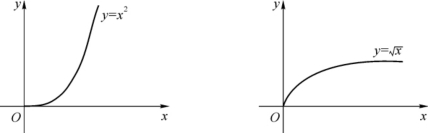
图3－9
若f（x）为上凹函数（见图3－10）.观察其图形不难发现其定义域内任何两点x1，x2（x1＜x2）所对应的曲线上面点A（x1，f（x1））B（x2，f（x2））之间的弦AB必然位于曲线上方.容易写出弦AB所在直线的方程为
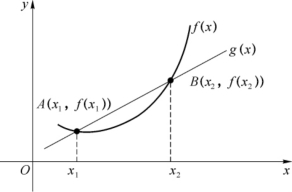
图3－10
以上位置关系表明对于任何x∈［x1，x2］，x在弦上的函数值g（x）不小于x在曲线上的函数值f（x），即
f（x）≤g（x）， x∈［x1，x2］.
由于［x1，x2］上任何一点x可表示为
x＝λx1＋（1－λ）x2， λ∈（0，1），
则x在弦AB上的函数值为
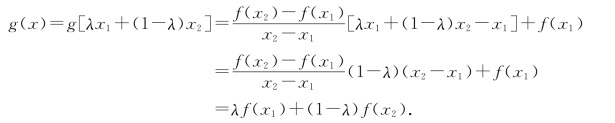
x在曲线上的函数值为
f（x）＝f［λx1＋（1－λ）x2］，
从而有
f［λx1＋（1－λ）x2］≤λf（x1）＋（1－λ）f（x2）.
用这个不等式定义上凹函数，并类似定义上凸函数.
定义1 设f（x）为区间I上的函数，若对I上任何两点x1，x2和任何实数λ∈（0，1），总有
f［λx1＋（1－λ）x2］≤λf（x1）＋（1－λ）f（x2），
则称f（x）为I上的上凹函数.如果总有则称f（x）为I上的上凸函数.
f［λx1＋（1－λ）x2］≥λf（x1）＋（1－λ）f（x2），
定理1 f（x）为区间I上的上凹（上凸）函数的充要条件是：对I上的任何三点x1＜x2＜x3（见图3－11），总有
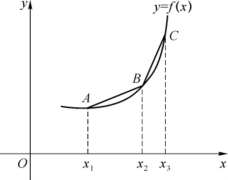
图3－11
结合图形不难理解此定理的几何意义，在此不再赘述.
证 只证上凹函数的情形.
（必要性） 设x2＝λx1＋（1－λ）x3，此时λ＝
.由上凹函数定义知
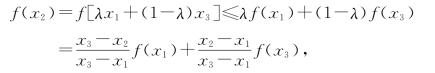
从而有
（x3－x1）f（x2）≤（x3－x2）f（x1）＋（x2－x1）f（x3），
将左端x3－x1换为（x3－x2）＋（x2－x1），整理后便得式（1）.
（充分性） 在I上任取两点x1，x3（x1＜x3），在（x1，x3）上任取x＝λx1＋（1－λ）x3，λ∈（0，1），此时λ＝
由式（1）易得
（x3－x1）f（x）≤（x3－x）f（x1）＋（x－x1）f（x3），
两边同除以x3－x1，得
f（x）＝f［λx1＋（1－λ）x3］≤λf（x1）＋（1－λ）f（x3），
即证得f（x）为上凹函数.
同理可证，f（x）为区间I上的上凹函数的充要条件是：对于区间I上任何三点，x1＜x2＜x3，有
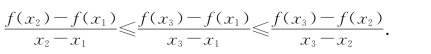
定理2 设f（x）为区间I上的可导函数，则f（x）为I上的上凹（上凸）函数的充要条件是：f′（x）在I上单调递增（递减）.
证 只证f（x）为上凹函数的情形.
（必要性） 设f（x）为区间I上的上凹函数，则对于I上任何两点x1，x2（x1＜x2）及任何x∈（x1，x2），有
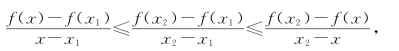
从而有
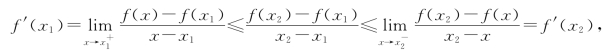
即f′（x）在I上单调递增.
（充分性） 设f′（x）在区间I上单调递增，任取区间I上三点x1＜x2＜x3，在［x1，x2］与［x1，x3］上分别利用拉格朗日中值定理，则存在ξ∈（x1，x2），η∈（x2，x3），使得
由以上定理知，f（x）在I上为上凹函数.
由以上定理可直接推得以下推论.
推论1 设f（x）在区间I上二阶可导，则f（x），为I上的上凹（上凸）函数的充要条件是
f″（x）≥0 （f″（x）≤0）， x∈I.
设f（x）在区间I上连续，x0为I的内点.如果曲线y＝f（x）在经过点（x0，f（x0））时，曲线的凸凹性改变了，此时称点（x0，f（x0））为曲线y＝f（x）的拐点.
若函数f（x）在区间I上可导且（x0，f（x0））为曲线y＝f（x）的拐点（x0为I的内点）.由极值的第一充分条件易知，x0为一阶导函数f′（x）的极值点；若f（x）还在x0有二阶导数，则必有f″（x0）＝0.故拐点在二阶导数不存在或等于0的点中产生.
例1 求f（x）＝（x－1）x2的凸凹区间及拐点.
3
解 该函数在第四节中讨论过其单调性与极值.同时，
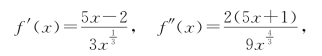
故当x＝0时，f″（x）不存在；x＝－
时，f″（x）＝0.凸凹区间及拐点列表如下.
故曲线的上凹区间为（－
，＋∞），上凸区间为（－∞，－
），拐点为（－
，－
）.