自变量趋于有限值时函数的极限
1.函数极限的定义
首先研究当自变量x→x0时函数f（x）的变化趋向.
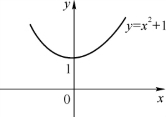
图1－12
考察函数f（x）＝x2＋1（见图1－12），由图可知，不论变量x从左侧还是右侧趋向于0时，函数值总是趋向于1.换言之，当x无限接近于0时，对应的函数值f（x）和常数1的差可以任意小.
类似于数列极限的定义，有如下定义.
定义1 设f（x）在点x0的某个去心邻域内有定义，如果对于任意给定的数ε＞0，总∃δ＞0，使得对满足不等式0＜
＜δ的所有x，其对应的函数值f（x）都满足
则称常数A为函数f（x）当x趋向于x0时的极限，记作
函数极限的几何意义：对于任意给定的ε＞0，都存在x0的一个去心邻域U （x0，δ）＝｛x
＜δ｝，当x∈U （x0，δ）时，曲线y＝f（x）上的点都位于两直线y＝A＋ε和y＝A－ε之间（见图1－13）.
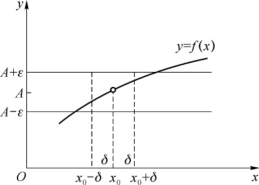
图1－13
注意 根据定义，函数在点x0的极限存在与否与函数在该点的函数值无关.另外，定义中的δ随ε而改变，对于同样的ε，由于x0不同，δ也会有变化.实际上，δ与x0和ε都有关，即δ＝δ（x0，ε）.
例1 用定义证明
＝2.
证 函数f（x）＝
在点x＝1无意义，但0在x0＝1的任何去心邻域内有定义.
对∀ε＞0，要使
只要取δ＝ε，则当0＜
＜ε成立.
所以
＝2.
例2 证明
＝1.
证 函数f（x）＝x2在点x0＝1的任意邻域内有定义，不妨取x0＝1的邻域为
＜1，从而有0＜x＜2，即有1＜x＋1＜3.
对∀ε＞0，要使
只要
成立.
所以，对于∀ε＞0，∃δ＝min
｝，当0＜
＜δ时，
＜ε成立.
从而有
＝1.
例3 证明
xsin
＝0.
证 函数f（x）＝xsin
在点x＝0无定义，但在x＝0的任何去心邻域内有定义.00
对∀ε＞0，要使
＜ε成立.
取δ＝ε，则当0＜
＜ε成立.
从而有
＝0.
2.函数极限的性质
函数极限与数列极限的性质类似，证明方法也相似，下面的定理由读者自行证明.
定理1 （极限的唯一性）若
f（x）存在，则极限唯一.
定理2 （函数的局部有界性）若
f（x）存在，则在x0的某一去心邻域内函数f（x）有界.
定理3 （函数的局部保序性）设
f（x）＝A，
g（x）＝B，若存在δ＞0，当x∈
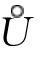（x0，δ）时，恒有f（x）≤g（x），则有A≤B.
推论 （函数的局部保号性）设
f（x）＝A，若存在δ＞0，当x∈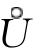
（x0，δ）时，恒有f（x）≤0，则有A≤0.
定理4 （函数极限与数列极限的关系）设f（x）在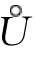
（x0，δ）上有定义，则
f（x）＝A的充分必要条件是对于任一收敛于x0的数列｛xn｝（xn≠x0），恒有
f （xn）＝A.
证 必要性：因为
f（x）＝A，则对任意ε＞0，总∃δ＞0，当0＜
＜δ时有
又因为
xn＝x0，所以对上述的δ＞0，∃N，当n＞N时有
又已知xn≠x0，故有
对满足此不等式的所有xn所对应的函数值f （xn），应有
由数列极限的定义知
f （xn）＝A.
充分性：反证法.若
f（x）≠A，则存在某个ε0＞0，对于∀δ＞0，总∃x′∈
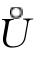（x0，δ），使得
特别取δ＝1，
，…，则存在x，x，x，…，使得当123
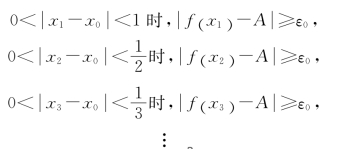
对上述xn∈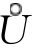
（x0，δ）形成的数列｛xn｝，显然有
xn＝x0（xn≠x0），且
≥ε0，即数列｛f （xn）｝不以A为极限，与假设矛盾.充分性得证.
该定理通常用来证明某些函数的极限不存在.
例4 证明当x→0时，sin
的极限不存在（见图1－14）.
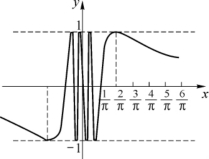
图1－14
证 取数列xn＝
（xn≠0），则有
x＝0，且n f （xn）＝0，即
f （xn）＝0.
再取数列x′n＝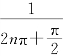
（x′n≠0），显然
x′n＝0，但是f （x′n）＝1，即
f （x′）＝1.n
对于同时收敛于0的两个不同数列，其对应的函数值数列收敛于不同的值.由定理4的充分性知，极限
sin
不存在.
3.单侧极限
在考察x→x0时函数f（x）的极限时，有时只需考察x从大于x0（即x0的右侧）的方向趋于x0时的极限，有时考察x从小于x0（即x0的左侧）的方向趋于x0时的极限，即函数f（x）在x0的左、右极限.
定义2 若函数f（x）在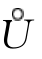
（x0，δ）上有定义，且对于∀ε＞0，总∃δ＞0，使得对满足不等式0＜x－x0＜δ（即x0＜x＜x0＋δ）的所有x，其对应的函数值f（x）都满足
则称常数A为函数f（x）当x趋向于x0时的右极限，记作
可类似定义函数f（x）当x趋向于x0时的左极限，只需把不等式0＜x－x0＜δ换成－δ＜x－x0＜0（即x0－δ＜x＜x0），记作
函数的左极限和右极限统称为单侧极限.
由函数极限的定义可得如下的结论.
定理5 函数f（x）在点x0存在极限的充分必要条件是：f（x）在x0的左、右极限都存在且相等.即
f（x）＝A⇔
f（x）＝
f（x）＝A.
例5 设f（x）＝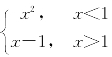
（见图1－15），求
f（x）.
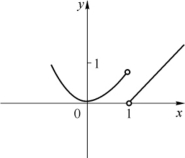
图1－15
解 f（x）在x＝1的左极限：
f（x）＝
x2＝1.f（x）在x＝1的右极限：
f（x）＝
（x－1）＝0.左、右极限存在但不相等，所以
f（x）不存在.