f（x）＝eλxP（x）（λ可以是复数，Pm（x）是m次多项式）
根据函数f（x）的特点，推测方程具有形如y＊＝Q（x）eλx的特解（其中Q（x）是某个待定的多项式）.由y＊＝Q（x）eλx，有
y＊′＝［Q′（x）＋λQ（x）］eλx， y＊″＝［Q″（x）＋2λQ′（x）＋λ2 Q（x）］eλx，
代入原方程，整理得
［Q″（x）＋（2λ＋p）Q′（x）＋（λ2＋pλ＋q）Q（x）］eλx＝Pm（x）eλx，
消去eλx，得
由特征多项式φ（r）＝r2＋pr＋q，知φ′（r）＝2r＋p.上式可简记为
注意到，方程（3）是关于多项式Q（x）的微分方程，只要设出Q（x）的一般形式，可利用比较系数的方法求出其各项系数.
例1 解微分方程y″－7y′＋12y＝x.
解 齐次方程为φ（r）＝r2－7r＋12＝0，解得r1＝3，r2＝4.
对应齐次方程的通解为
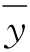＝C1e3x＋C2e4x，其中C1，C2为任意常数.
设原方程特解为y＊＝Q（x），将φ（0）＝12，φ′（0）＝－7，Pm（x）＝x代入方程（2）得
Q″（x）－7Q′（x）＋12Q（x）＝x，
比较等式两边次数，Q（x）应为一次多项式.设Q（x）＝ax＋b，则
－7a＋12（ax＋b）＝x，
比较系数得
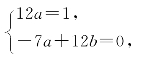
解得a＝
因此原方程的一个特解为
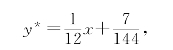
故原方程的通解为
依照上面分析，也可以直接写出Q（x）的具体待定形式.事实上，由（2）式知：
若λ不是特征根，则λ2＋pλ＋q≠0，故Q（x）应为m次多项式，可设特解y＊＝Qm（x）eλx＝（a0xm＋a1xm－1＋…＋am），eλx（a0，a1，…，am为特定系数）；
若λ是特征根并且为单根，则λ2＋pλ＋q＝0，但2λ＋p≠0，若Q′（x）应为m次多项式，可设特解y＊＝xQm（x）eλx＝x（a0xm＋a1xm－1＋…＋am）eλx（a0，a1…，am为待定系数）；
若λ是特征根，且为二重根，则λ2＋pλ＋q＝0，且2λ＋p＝0，故Q″（x）应为m次多项式，可设特解y＊＝x2 Qm（x）eλx＝x2（a0xm＋a1xm－1＋…＋am）eλx（a0，a1，…，am为待定系数）.
综上，非齐次线性方程特解设法为考虑方程
其对应的齐次方程为
特征方程为
于是可设方程（4）的特解为
其中Qm（x）＝a0xm＋a1xm＋…＋am，（a0，a1，…，am为待定系数）.
k取值由λ是特征方程（6）的k重根决定，k＝0，1，2.
接下来，用比较系数方法可以求出a0，a1，…，am从而写出方程（4）的特解.
例2 解微分方程y″＋4y′＋4y＝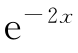
.
解 特征方程φ（r）＝r2＋4r＋4＝0，解得r＝－2（重根）.对应的齐次微分方程的通解为
其中C1，C2为任意常数.
由于－2是二重根，可设原方程特解为
y＊＝e－2x·x2·A，
于是
（y＊）′＝（2xA－2x2 A）e－2x， （y＊）″＝（2A－8xA＋4x2 A）e－2x，
代入原方程得
因此原方程的一个特解为
故原方程的通解为
