隐函数求导法则
前面讨论了函数y＝f（x）的求导方法，但有时函数关系是通过方程给出的，如
x＋y3＝1，
解出其函数表达式为y＝
，称为显函数.若不解出y，方程x＋y3＝1仍然隐含有上述函数关系，此时称函数关系y＝y（x）是隐函数.
一般来说，若函数y＝f（x）可使二元方程F（x，y）＝0成立，即F［x，f（x）］≡0，则称y＝f（x）是由方程F（x，y）＝0所确定的隐函数.
对一给定的方程F（x，y）＝0，要求出y＝f（x）并非易事，有时也没有必要，下面讨论由F（x，y）＝0所确定的隐函数y＝f（x）的求导问题.
例1 求由方程ey＋xy－e＝0所确定的隐函数y的导数
解 方程两边对x求导，得
考虑到y＝y（x），再由复合函数求导法，有
解之得
当x＝0时，y＝1，代入上式，得
例2 求由方程x2＋y2＝1所确定的隐函数y＝y（x）的导数
及二阶导数
解 方程两边对x求导，得
有
再对x求导，得
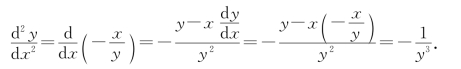
例3 证明：过双曲线
＝1上一点（x0，y0）的切线方程是
证 先求切点（x0，y0）的切线斜率k，即由双曲线所确定的隐函数y＝f（x）在该点的导数值.
方程两边对x求导，得
即
所以，切点（x0，y0）处的切线斜率k＝
，切线方程为
整理得
又（x0，y0）在双曲线上，所以所求切线方程为
有些函数虽为显函数，但直接求导比较烦琐或是不易求导，这时可采用下述的对数求导法.
例4 求幂指函数y＝u （x ）v（x）的导数
（u（x）＞0）.
解 方程两边取对数，得
ln y＝v （x ）lnu （x），
此方程隐含函数关系y＝y（x），两边对x求导，得
所以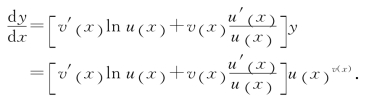
另外，此题也可化成复合函数y＝
后求导，请读者用此方法验证上述结论.特别地，取u（x）＝v（x）＝x，则有
（xx）′＝xx （lnx＋1 ）（x＞0）.
例5 设y＝xtan x （x＞0），求
解 两边取对数，得
ln y＝tan xln x，
两边对x求导，得
所以
例6 设y＝
，求y′.
解 上式两边取对数，得
对x求导，得
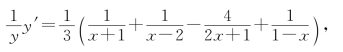
所以
