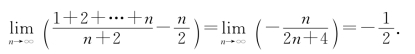极限的四则运算

一、极限的四则运算

定理1 设在x的某种趋向下，limf（x）＝A，limg（x）＝B，则有

（1）lim ［f（x）±g（x）］＝limf（x）±limg（x）＝A±B；

（2）lim ［ff（x）g（x）］＝limf（x）limg（x）＝AB；

（3）lim，其中B≠0.

证 因为limf（x）＝A，limg（x）＝B，所以

f（x）＝A＋α（x）， g（x）＝B＋β（x），

其中，limα（x）＝limβ（x）＝0.

（1）因为f（x）±g（x）＝（A±B）＋［α（x）±β（x）］.

由无穷小量的性质知　lim［α（x）±β（x）］＝0，所以lim　　［f（x）±g（x）］＝A±B＝limf（x）±limg（x）.

（2）因为

ff（x）g（x）＝［A＋α（x ）］［B＋β（x）］＝AB＋Bα（x）＋Aβ（x）＋α（x）β（x）.

由于　　lim ［Bα（x）＋Aβ（x）＋α（x）β（x）］＝0，所以　　lim ［ff（x）g（x）］＝AB＝limf（x）limg（x）.

（3）因为

由于limβ（x）＝0，所以存在x的某个邻域，使得在此邻域内，故有

所以

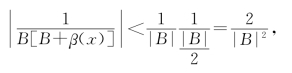
而

lim ［Bα（x）－Aβ（x）］＝0，

所以

即有lim，其中B≠0.

推论1 若limf（x）＝A，C为任意常数，则lim ［Cf（x）］＝Climf（x）＝CA.

推论2 若limf（x）＝A，n是正整数，则limfn（x）＝［limf（x ）］n＝An.

推论3 若f（x）≥0，且limf（x）＝A≥0，n为正整数，则lim

证 因为A＝limf（x）＝lim，所以lim

数列也有类似的结论.

定理2 设有数列｛xn｝，｛yn｝，且有 xn＝A

yn＝B，则有

（1）（xn±yn）＝ xn±yn＝A±B；

（2）（xnyn）＝yn＝AB；

（3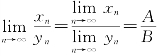），其中B≠0，且yn≠0（n＝1，2，…）.

证明从略.

定理3 若在x的某变化区间内有f（x）＞g（x），且limf（x）＝A，limg（x）＝B，则有A≥B.

证 因为在x的某变化区间内有f（x）＞g（x），此时f（x）－g（x）＞0.

由函数极限的性质知0≤lim ［f（x）－g（x）］＝limf（x）－limg（x）＝A－B，所以A≥B.

例1 求 （x2－5x＋2）.

解 （x2－5x＋2）＝x2－5x＋2＝（－1）2－5（－1）＋2＝8.

例2 求

解 函数分子、分母的极限都存在，且分母的极限不为零，所以

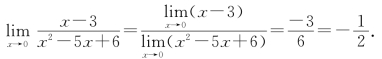
例3

解 当x→3时，分子分母的极限都为零，不能直接应用极限的四则运算法则.此时考虑先对函数进行化简，

例4 求（a0xn＋a1xn－1＋…＋an－1x＋an），其中a0≠0.

解 不满足每一项的极限都存在的条件，所以不能直接用四则运算法则.考虑多项式函数的倒函数的极限，即

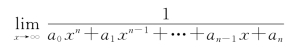
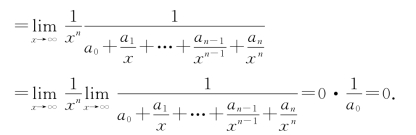
由于无穷小量的倒函数的极限为无穷大量，所以

例5 求

解 由例4知，（2x2＋x＋3）＝∞，（3x2－x＋2）＝∞.

函数分子分母的极限都不存在，但可以考虑把分子分母同除以x的最高次幂x2，然后再求极限.

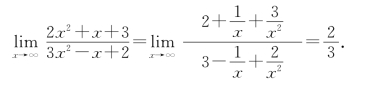
例6 求

解 先对函数进行分子有理化，再求极限，即

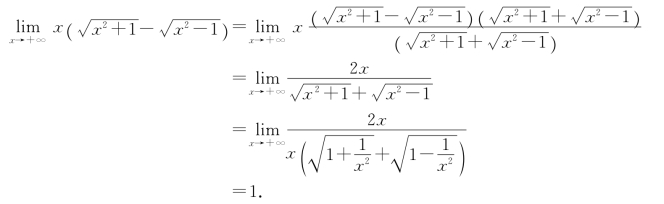
例7 求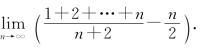

解 因为1＋2＋…＋n＝，所以

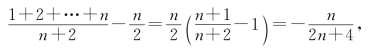
从而有