导数的几何意义

二、导数的几何意义

由前面的讨论可知：函数y＝f（x）在点P（x0，y0）处可导，则P（x0，y0）点处的切线斜率k即为函数在该点处的导数值f′（x0），也就是k＝f′（x0）.由于该点处的切线和法线相互垂直，所以P点处的法线斜率为－（f′（x）≠0）.点P处的切线方程和法线方程如下.0

切线方程：

y－y0＝f′（x0）（x－x0）.

法线方程：

若函数y＝f（x）在点x0处的导数不存在，但函数变化率→∞（当Δx→0时），这时，函数在（x0，f （x0））处具有铅直切线x＝x0.例如y＝，在点x＝0处不可导，但在（0，0）点处有切线x＝0（即y轴）.

例5 求曲线y＝sin x在点处的切线方程和法线方程.

解 因为（sinx）′＝cos x，所以切线斜率

法线斜率

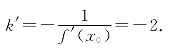
所以点）处的切线方程：y－，即y＝

法线方程：y－＝－2（x－），即y＝－2x＋