二、基本定义
定义1 含有自变量、未知函数及其导数或微分的方程称为微分方程，并把只含一个自变量的微分方程叫作常微分方程，含有多个自变量的微分方程叫作偏微分方程.本章所介绍的为常微分方程.引例的（1）式和（4）式是常微分方程的简单例子，较复杂的例子如：
定义2 微分方程中出现导数的最高阶数称为微分方程的阶.
例如，（1）式和（9）式都是一阶微分方程，（10）式可化为
＋xy＝0，因而也是一阶微分方程.（4）式和（11）式都是二阶微分方程。
n阶常微分方程的一般形式可写为
其中y（n）必须出现，而x，y，y′，…，y（n－1）等变量可以不出现.方程（12）为隐式的n阶方程，若能从此方程中解出最高阶导数即
则方程（12′）为显示表示的n阶常微分方程.
定义3 如果方程中出现的未知函数及其各阶导数，对每一个加项而言累计只是一次，称它为线性微分方程.
例如，方程（1）和方程（4）以及方程（9）、（10）、（11）均为线性微分方程，而像（y″）2＋y′＝0，y′＋siny＝0为非线性微分方程.
定义4 如果方程中未知函数或其导数的系数不依赖于自变量，称它为常系数微分方程，否则称为变系数微分方程.
例如，方程（1）、（4）、（11）是常系数微分方程，而方程（9）、（10）是变系数微分方程.
定义5 如果将某一函数代入微分方程能使其成为恒等式，则称这个函数为微分方程的解.
例如，（3）式和（3′）式都是方程（1）的解，（8）式和（8′）式都是方程（4）的解.
如果微分方程的解中含有独立的任意常数等于该微分方程的阶数，称这种解为微分方程的通解.
所谓独立任意常数的个数，指的是对所得的解表达式重新整理（如代数、三角恒等式变形、同类项合并）所得的最少的任意常数的个数.例如，C1x＋C2y＋C3＝0可变形为y＝C1x＋C2，y＝asin2 x＋bsin2 x＋ccos2x可化为y＝C1cos2 x＋C2sin2 x，均为只有两个任意常数.
引例中，（3）式是方程（1）的通解，（8）式是方程（4）的通解.
微分方程不含任意常数的解称为方程的特解.例如（3′）式是方程（1）的特解，（8′）式是方程（4）的特解.
求微分方程满足初始条件的解的问题称为初值问题.一般地，n阶常微分方程的初值问题可记作：
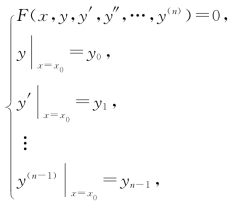
其中x0，y0，y1，…，yn－1都是已知常数.
例如，一阶微分方程的初值问题，可记作
方程（13）的解的图形是一条曲线，叫作微分方程的积分曲线.初值问题（13）的几何意义，就是求微分方程通过点（x0，y0）的那条积分曲线.
例3 验证y＝C1cos x＋C2sin x是方程y″＋y＝0的通解，并求此方程满足初始条件y（
）＝1，y′（
）＝－1的特解，其中C1，C2是常数.
解 因为y＝C1cos x＋C2sin x，所以
y′＝－C1sin x＋C2cos x， y″＝－C1cos x－C2sin x，
从而有y″＋y＝0，且C1，C2是互相独立的任意常数，即y＝C1cos x＋C2sin x是方程y″＋y＝0的通解.
将初始条件代入通解，得
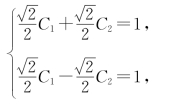
解出C1＝
，C2＝0，故所求满足初始条件的解为y＝