定积分在几何上的应用

二、定积分在几何上的应用

1.平面图形的面积

在直角坐标系下，利用定积分的几何意义容易推出由连续曲线f（x），直线x＝a，x＝b（a＜b）和x轴所围成的平面图形的面积有以下公式.若f（x）非负，则所围图形的面积为

如果f（x）在［a，b］上不为非负函数，则所围图形的面积为

一般地，由两条连续曲线y＝f（x），y＝g（x）以及直线x＝a，x＝b（a＜b）围成的平面图形的面积为

例1 求由曲线y＝2，y＝x及xy＝1所围平面图形的面积（见图5－10）.

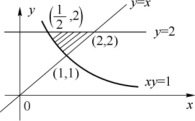
图5－10

解 （方法一） 对x积分

（方法二） 在对y积分

在极坐标系下，（见图5－11）由连续曲线r＝φ（θ）及射线θ＝α，θ＝β围成的平面图形的面积为

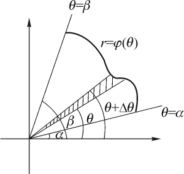
图5－11

事实上，利用元素法，取极角θ为积分变量，其变化范围为［α，β］.在任一小区间［θ，θ＋Δθ］上的小曲边扇形的面积可近似用半径为φ（θ）的扇形面积来代替，即当Δθ→0时

对上式积分，有

例2 求双纽线r2＝a2ω＞2θ所围平面图形的面积（见图5－12）.

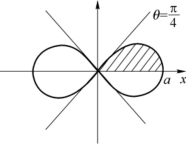
图5－12

解 由图形的对称性可知

若平面图形由参数方程表示的曲线围成，曲线Γ的参数方程为x＝x（t），y＝y（t），α≤t≤β，其中x（t），y（t）在［α，β］上连续，x（t）有连续的导函数且x（t）≠0.记a＝x（α），b＝x（β）则由曲线Γ，直线x＝a，x＝b以及x轴围成的平面图形的面积为

事实上，由x′（t）≠0知x′（t）在［α，β］上恒正或恒负，从而x（t）严格单调，若x（t）严格单增，则此时a＜b，设t＝t（x）为x＝x（t）的反函数.

则曲线方程可表为

y＝y［t（x）］，

从而所用图形的面积为

若x（t）严格单减，此时b＜a，所用图形面积为

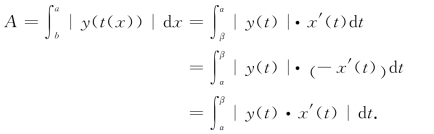
例3 求由星形线x＝acos3 t，y＝asin3 t，0≤t≤2π所围成的图形的面积（见图5－13）.

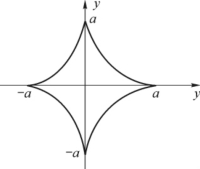
图5-13

解 由对称性

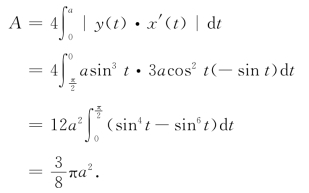
2.体积

（1）旋转体的体积

由一个平面图形绕此平面内一直线旋转一周而成的立体叫旋转体.这条直线叫旋转轴.圆柱、圆锥、圆台、球体都是旋转体.

用元素法求图5－14中旋转体的体积.

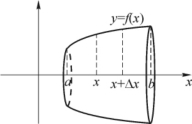
图5－14

取横坐标x为积分变量，其变化范围为［a，b］.对任一小区间［x，x＋Δx］⊂［a，b］上旋转体薄片的体积近似等于以f（x）为底面半径、dx为高的圆柱体的体积：

dV＝π［f（x）］2dx，

再在闭区间上积分，便得旋转体的体积：

例4 计算由椭圆

所围图形绕x轴旋转一周而成的立体（椭球体）的体积.

解 第一象限内椭圆线方程为

利用对标性，有

例5 求底面半径为r，高为h的圆锥的体积.

解 如图5－15所示，建立坐标系.圆锥可看作由直线y＝－与坐标轴所围图形绕y轴一周而成的旋转体.

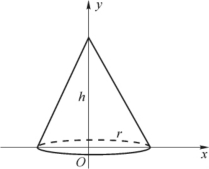
图5－15

从而

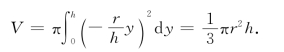
（2）由平行截面所截立体的体积

如图5－16所示，设立体位于过x＝a与x＝b垂直于x轴的两平面之间，用过x点垂直于x轴的平面截得的截面面积为A（x）。假设A（x）为［a，b］上的连续函数，取x为积分变量，对应于区间［x，x＋Δx］的薄片的体积近似等于以A（x）为底面面积，高为Δx的圆柱体的体积，即体积元素

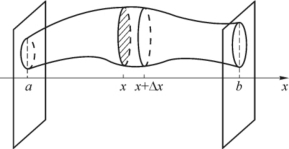
图5－16

dv＝A（x）dx.

以A（x）dx为被积表达式，在［a，b］上积分，便得此体体积为

例6 求由两个圆柱面x2＋y2＝a2与y2＋x2＝a2所围立体的体积（见图5－17）.

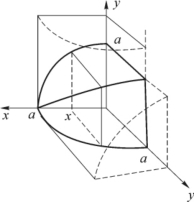
图5－17

解 任取x∈［0，a］，平面x＝a截此主体第一卦限部分的截面积为

从而立体体积为

3.平面曲线的弧长与曲率

（1）平面曲线的弧长

设平面曲线C＝（如图5－18所示），在C上依次取分点

A＝P0，P1，…，Pn＝B，

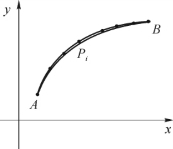
图5－18

并依次连接相邻分点得一折线，当分点增多且每个小段都缩向一点时，如果此折线长

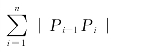
的极限存在，称此极限为曲线AB的弧长，并称此曲线是可求长的.

若曲线上每点都有切线，且切线随切点移动而连续转动，称这样的曲线为光滑曲线.

定理 光滑曲线是可求长的.

（证明略）

若光滑曲线C由参数方程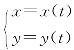（t）给出，其中x（t），（t）均在［，］上有连续α≤≤βyαβ导数，且x′（t），y′（t）不同时为0.我们用元素法来求曲线C的长度.

取参数t为积分变量，变化范围为［α，β］，在［α，β］内任一小区间［t，t＋Δt］上对应的小弧段的长度Δs近似等于对应的弦的长度由于

Δx≈dx＝x′（t）dt，Δy≈dy＝y′（t）dt.

从而弧长表示为

积分便得弧长公式

若曲线C由直角坐标方程

y＝f（x） （a≤x≤b）

给出，其中f（x）在［a，b］上有连续导数，这时曲线的弧长为

若曲线C由极坐标方程

ρ＝ρ（θ） （α≤θ≤β）

给出，其中ρ（θ）在［α，β］上有连续导数，则曲线的弧长公式为

事实上，将曲线的极坐标方程化为直角坐标系下以θ为参数的参数方程

从而可得弧长公式为

例7 求摆线x＝a（t－sint），y＝a（1－cos t）（a＞0）一拱的弧长（见图5－19）.

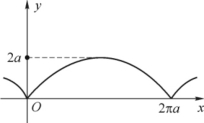
图5－19

解 由x′（t）＝a（1－cos t），y′（t）＝asint，则有

例8 求心形线r＝a（1＋cosθ）（a＞0）的周长（见图5－20）

解 由r′（θ）＝－asinθ，并注意到对称性，有

（2）曲率

这里将引入曲率的概念，它表示平面曲线上各点处的弯曲程度.考察图5－21会发现，弧段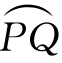与等长，但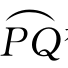弯曲程度较要大，这是由于动点从P移至Q时，切线旋转过的角度要此动点从Q移至R时切线旋转的角度要大的原因.

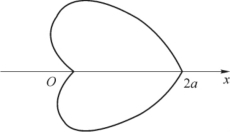
图5－20

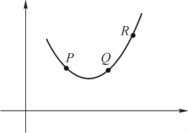
图5－21

设当滑曲线由参数方程x＝x（t），y＝y（t），α≤t≤β给出，α（t）表示曲线在点p（x（t），y（t））处的切线的倾角，Δα＝α（t＋Δt）－α（t）表示动点由P沿曲线移至Q（x（t＋Δt），y（t＋Δt））时切线倾角的增量.若弧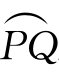之长为Δs，则称

为弧段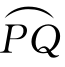的平均曲率.如果存在极限

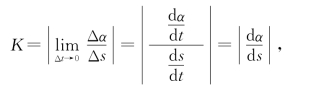
称此极限K为曲线在点P处的曲率.

由于

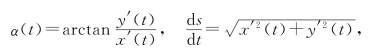
则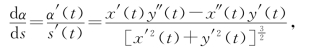

从而

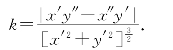
若曲线由方程y＝f（x）给出，则有

若曲线由极坐标方程r＝r（θ）给出，则有

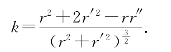
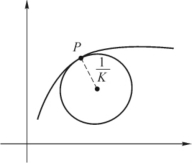
图5－22

设曲线上点P处的曲率为K≠0.若过点P从一个半径为ρ＝的圆，使它与曲线在P处有相同的切线，并在P的近旁，此圆与曲线在切线的同侧，我们称此圆为曲线在点P处的曲率圆（见图5－22）.曲率圆的半径P＝称为曲线在P处的曲率半径.由曲率圆的定义可知，曲率圆与曲线在点P处有相同的曲率和切线，并有相同的凹凸性.

例9 抛物线y＝ax2＋bx＋c（a＞0）上哪点处的曲率最大？

解 由y′＝2ax＋b，y″＝2a，从而

当x＝－时，分母最小，K有最大值2a.即抛物线与其顶点处曲率最大.