连续函数的性质

三、连续函数的性质

根据极限的四则运算法则及函数的连续性定义，可得连续函数的四则运算定理.

定理1 设函数f（x）与g（x）都在点x0连续，则

也在点x0连续.（证略）

定理2 若函数y＝f（x）在某区间I上连续，且严格单调增加（减少），则其反函数x＝f－1（y）在对应区间上也连续，并且严格单调增加（减少）.（证略）

定理3 若函数y＝f（u）在点u0连续，u＝φ（x）在点x0连续，且u0＝φ（x0），则复合函数y＝f［φ（x）］在点x0连续.

证 因为y＝f（u）在点u0连续，所以，∀ε＞0，∃η＞0，当＜η时有

又因为u＝φ（x）在点x0连续，所以对上述η＞0，∃δ＞0，当x－x0＜δ时有

综合（1）和（2）知，对∀ε＞0，∃δ＞0，当＜δ时有

恒成立，从而知y＝f［φ（x）］在点x0连续.

根据上述定理的证明方法，可得如下结果：

若函数y＝f（u）在点u＝a连续，u＝φ（x），且φ（x）＝a，则复合函数的极限f［φ（x）］存在，且

例7 证明

证 由对数函数的连续性及重要极限＝e可知，

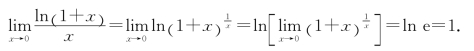
根据定理3及对数函数、指数函数的连续性可得到关于幂指函数f的极限求法.

推论1 设limf（x）＝A＞0，limg（x）＝B，则limff＝AB.其中，lim表示对x→x0，x→∞等趋向都成立.

证 令u （x）＝ff，则u （x）＝

又

所以

例8 求

解 因为

所以

由于初等函数是由基本初等函数经过有限次四则运算及复合而得，所以初等函数在其定义区间上连续.

例如，f（x）＝ln在其定义区间（－∞，2）上连续；函数f（x）＝的定义域为D＝不构成区间，f（x）在其定义域上每一点都不连续，即f（x）在D上处处不连续.