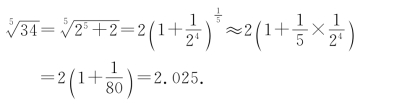微分在近似计算中的应用

四、微分在近似计算中的应用

设函数y＝f（x）在点x0处可微，当很小时，有

Δy≈dy＝f′（x0）Δx，

即

Δy＝f （x0＋Δx）－f （x0）≈f′（x0）Δx

或

f（x）≈f （x0）＋f′（x0）（x－x0），

即在x0的邻域内，可用切线上的值近似代替曲线上的值（以直代曲）.

当x0＝0时，

f（x）≈f（0）＋f′（0）x，

由此，可推得几个常用的近似公式（当充分小时）：

（1）sin x≈x；　　（2）tan x≈x；

（3）ex≈1＋x； （4）ln （1＋x）≈x；

（5）≈1－x；（6）

以上公式容易证明，现只证

设f（x）＝，有f（0）＝1，那么

代入f（x）≈f（0）＋f′（0）x中，即得

例5 有一批半径为1cm的球要镀一层铜，厚度为0.01cm，估计每个球需用铜多少克（铜的密度是8.9g／cm3）？

解 球的体积为

当R0＝1，ΔR0＝0.01时，

ΔV≈V′（R0）ΔR＝4πR2ΔR＝4×3.14×12×0.01＝0.13cm3，

于是每个球需镀铜约

8.9×0.13＝1.16g.

例6 求sin 31°的近似值.

解 取f（x）＝sin x，x0＝30°＝，Δx＝1°＝，所以

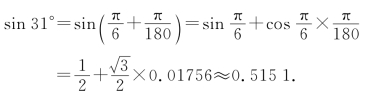
例7 求的近似值.

解 当很小时，有