一、导数的定义
导数的概念和数学的其他概念一样，也是客观世界中的自然现象在数量关系上的抽象.物体运动的瞬时速度、曲线的切线斜率、电路中的瞬时电流等都可以用函数的导数来表示.为引入导数的概念，先对以下两个具体实例进行分析.
实例1 电流问题
设有电流通过一导线，从时刻t＝0到时刻t之间通过该导线横截面的电量Q是时刻t的函数Q （t）.设时刻t0的电量为Q （t0），当t0有一个改变量Δt时，相应的电量Q也有一个改变量ΔQ，即在Δt时间段内通过导线横截面的电量为
比值
表示在Δt时间段内通过导线的平均电流.Δt越小，比值
越接近t0时刻的电流，所以当极限
存在时，其极限值即为t0时刻的瞬时电流.
实例2 切线斜率问题
设有平面曲线（如图2－1所示），它的方程为y＝f（x），现求曲线上一点P（x0，y0）的切线斜率.为求P点处的切线，可以先考虑P点处的割线.在曲线上任取一点Q，其横坐标为x0＋Δx，纵坐标为f （x0＋Δx）.设割线
与x轴的夹角为θ，则割线斜率
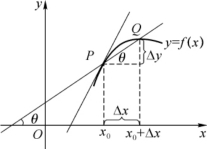
图2－1
上式比值表示曲线y＝f（x）在x0附近的区间内的平均变化率.Q点越靠近P点，割线斜率
越逼近P点处的切线斜率，因此当极限
存在时，极限值即为所求P点处的切线斜率.
以上两例，一个是物理学中的电流问题，一个是几何学中的切线斜率问题.虽然所表示的实际意义不同，但它们在数学上的表达形式却完全相同，即都是函数的改变量Δy与自变量的改变量Δx的比值的极限（Δx→0）.它们表示的都是函数对自变量的变化率.这一共性可抽象成如下的定义.
定义1 设函数y＝f（x）在点x0的某个邻域内有定义，对自变量的任一改变量Δx，函数相应的改变量为Δy，若极限
存在，则称此极限值为函数y＝f（x）在点x0处的导数，记作
此时称函数y＝f（x）在点x0可导；若上述极限不存在，则称函数y＝f（x）在点x0不可导，或称y＝f（x）在点x0的导数不存在.
有了函数导数的定义，则瞬时电流即为电量Q （t）在时刻t0处的导数，即Q′（t0）；切线斜率则可表示成函数y＝f（x）在点x0处的导数f′（x0）.
导数的定义还有如下的等价形式：
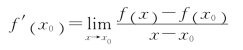
或
如果函数在某区间（a，b）内每一点都可导，则称函数在区间（a，b）内可导，并将
称为y＝f（x）的导函数.导函数也常记为f′（x），y′（x），
或
显然，若函数y＝f（x）在（a，b）内可导，则函数在点x0处的导数值等于导函数在点x0处的值，即
若函数在区间（a，b）内可导，且导函数f′（x）在（a，b）内连续，则记为
下面从导数的定义出发，求出几个基本初等函数的导函数.
为书写方便，常省略导函数中的变量记号，如记y′＝y′（x），f′＝f′（t）等.
例1 设y＝f（x）＝C（C为常数），则y′＝0.
证
即常数的导数等于零.
例2 设y＝sin x，则y′＝cos x.
证
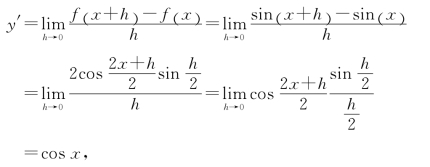
即
用同样方法可得
例3 设y＝ax（a＞0，a≠1），则y′＝axln a.
证
令t＝ah－1，则h＝loga（1＋t），且由函数y＝ax的连续性知，当h→0时，有t→0.故
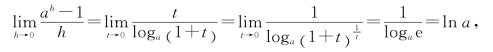
所以
y′＝ax·ln a，
即
（ax）′＝axln a.（xα）′＝αxα－1 x≠（0）.
当a＝e时，（ex）′＝ex.
例4 设y＝xα（α为任意实数），则y′＝αxα－1 （x≠0）.
证 当x≠0时，y′＝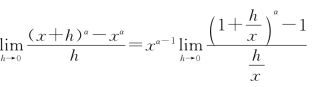
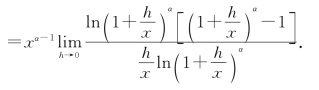
令t＝（1＋
α，则当时，此时）－1h→0t→0
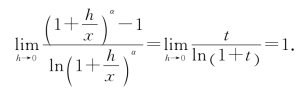
再令s＝
，显然有h→0时s→0，故
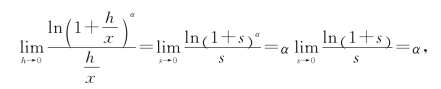
所以
事实上，当x＝0时，用导数定义，有
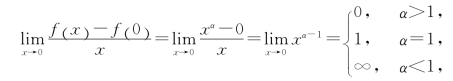
即当α＜1时，函数在x＝0点不可导.
当α＝n（n为自然数）时，有（xn）′＝nxn－1；
当α＝
时，
＝
当α＝－1时，（
）′＝－