微分的运算法则

二、微分的运算法则

由前面讨论知，当函数在点x可导时，函数必在点x可微，且dy＝f′（x）dx.根据基本初等函数的导数公式和导数运算法则，相应地可得到基本初等函数的微分公式和微分运算法则.

1.基本微分表

2.微分的运算法则

设u＝u（x），v＝v（x）在点x处可微，则

（1）d（u±v）＝du±dv；

（2）d（Cu）＝Cd（u）（C为常数）；

（3）d（uv）＝udv＋vdu；

（4）（v≠0）；

（5）复合函数的微分

设y＝f（u）对u可导，u＝φ（x）对x可导，则复合函数y＝f［φ（x）］在点x处可微，其微分为

dy＝f′［φ（x）］φ′（x ）dx＝f′（u ）du，

也就是说，不论u是自变量还是中间变量，其微分形式是一样的，这一性质称作一阶微分的形式不变形.

类似于高阶导数，可定义高阶微分.

二阶微分：d2 y＝d （dy）＝d［f′（x ）dx］＝［df′（x ）］dx＝f″（x ）（dx ）2＝f″（x）dx2.

三阶微分：d3 y＝d （d2y）＝f‴（x ）dx3.

一般而言，n阶微分dny＝d （dn－1y）＝f（n）（x ）dxn与n阶导数＝f（n）（x）是一样的，即函数的高阶可微性就是它的高阶可导性.

注意区别下面记号：（dx ）2表示x的微分的平方，简记成dx2；d （x2）是x2的微分，即2xdx；d2 x是x的二阶微分，即d （dx）.

例3 设y＝，求dy.

解 （方法1）

所以

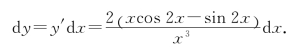
（方法2）运用微分的运算法则，得

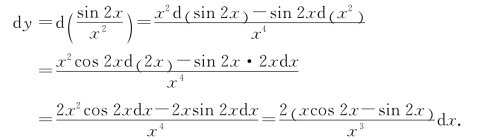
例4 在下列等式右端的括号内填入适当的函数.

（1）x2dx＝d（　）； （2）dx＝d（　）； （3）5xdx＝d（　）.

解 （1）x2dx＝d（x3＋C）； （2）dx＝d （2＋C）；

（3）5xdx＝d（＋C），其中，C为常数.