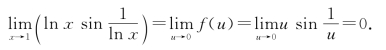二、复合函数的极限运算法则
定理4 设y＝f（u），u＝φ（x）.若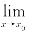
φ（x）＝a（在x0的某去心邻域内φ（x）≠a），且
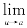f（u）＝A，则复合函数f［φ（x）］在点x0的极限存在，且
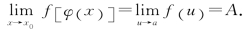
证 因为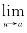
f（u）＝A，所以对∀ε＞0，∃η＞0，当0＜
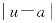＜η时，有
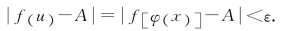
设当x∈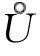
（x0，δ0）时φ（x）≠a，又因为
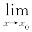φ（x）＝a，对上述η＞0，∃δ1＞0，当0＜
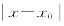＜δ1时，有
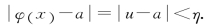
综上所述，∀ε＞0，∃δ＝min｛δ0，δ1｝＞0，当0＜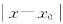
＜δ时，
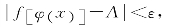
即
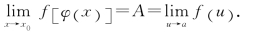
例8 求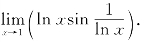
解 设u＝ln x，则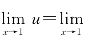
ln x＝0，而ln xsin
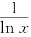＝f（u）＝usin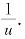
由复合函数极限运算法则知
