可化为齐次方程的方程

二、可化为齐次方程的方程

方程

当C＝C1＝0时是齐次方程，否则不是齐次方程.

在非齐次方程情况下想借助于齐次方程解决，解题基本思路是首先替换变量，即

其中h及k是待定常数.

此时，原方程化为

要使方程（5）为Y关于X的齐次方程，只须选取适当h和k，使

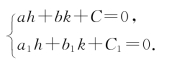
（1）当ab1≠a1b时，由克拉默法则可解出唯一的h及k满足上述条件.

此时方程（5）化为齐次方程

求出它的通解，再以x－h代替X，以y－k代替Y，便得原方程的通解.

（2）当ab1＝a1b时，可令＝λ，那么原方程（3）可写为

引入新的未知函数v＝ax＋by，可得

于是，原方程变为

为可分离变量型方程.

以上所介绍的方法可用于更一般的方程，即

例2 解方程（x－y＋1）dx－（x＋y－3）dy＝0.

解 方程化为

令x＝X＋h，y＝Y＋k，代入上式得

令h，k满足方程

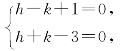
解得h＝1，k＝2，所以

x＝X＋1，y＝Y＋2，

因此，原方程化为

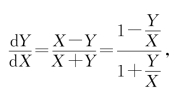
是齐次方程.可令u＝，则

代入，整理得

分离变量，得

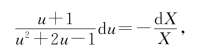
两边积分，得

即

Y2＋2 XY－X2＝C.

以X＝x－1和Y＝y－2代回，得原方程通解为

（y－2）2＋2（x－1）（y－2）－（x－1）2＝C （C为任意常数）.