一、函数的概念
定义1 设D是一个给定的数集，如果对于每个数x∈D，按照一定法则f总有确定的数值y与之对应，则称y是x的函数，记作y＝f（x）.数集D称为这个函数的定义域，x称为自变量，y称为因变量.
当x取数值x0∈D时，与x0对应的y的数值称为函数y＝f（x）在点x0处的函数值，记作f （x0）；当x取遍数集D的每个数值时，对应的函数值全体组成的数集R＝｛
＝f（x），x∈D｝称为函数的值域.
函数y＝f（x）中表示对应关系的记号f也可以改用其他字母表示，如φ，g，F等.这时，函数就相应地记为y＝φ（x），y＝g（x），y＝F （x）等.
在实际问题中，函数的定义域根据问题的实际意义而确定.在数学研究中，有时不考虑函数的实际意义，而抽象地用算式表达函数.这时约定：函数的定义域就是自变量所能取得的使算式有意义的一切实数。例如，函数y＝
的定义域是闭区间［－1，1］；函数y＝
的定义域是开区间（－1，1）.
如果自变量在定义域内任取一个数值时对应的函数值总是只有一个，这种函数称为单值函数，否则称为多值函数.
本书凡没有特别说明，本书中的函数总是指单值函数.
函数的表示方法主要有三种形式：解析法（用公式表示）、表格法、图形法.图形法是表现函数特性最直观的方法，用直角坐标平面上的点集
表示函数y＝f（x），x∈D的图形（见图1－3）.
下面举例说明.
例1 函数y＝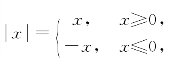
的定义域D＝（－∞，＋∞），值域R＝［0，＋∞），图形如图1－4所示.
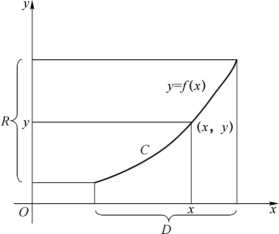
图1－3
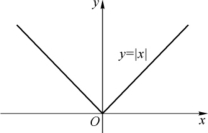
图1－4
例2 函数
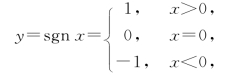
称为符号函数.这种分区间表示的函数称为分段函数.它的定义域D＝（－∞，＋∞），值域R＝｛－1，0，1｝，图形如图1－5所示.对于任何实数x，关系式x＝sgn x·
成立.
例3 设x为任一实数，不超过x的最大整数记为［x］.函数y＝［x］的定义域D＝（－∞，＋∞），值域R＝Z为所有整数，图形如图1－6所示.这个函数又称为取整函数.
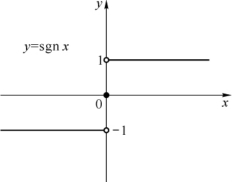
图1－5
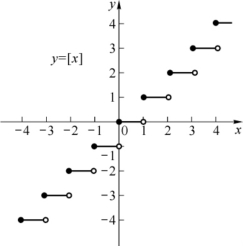
图1－6
例4 设f（x）＝
，求f （x＋Δx）－f（x）.
解 f （x＋Δx）－f（x）＝