二、极值
在第一节中，费马定理说明函数f（x）在可导点x0处取极值的必要条件为f′（x0）＝0.下面再给出函数取极值的两个充分条件.
定理3（极值第一充分条件） 设函数f（x）在x0点连续，且在其某邻域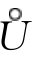
（x0，δ）内可导.
（1）当x∈（x0－δ，x0）时，f′（x）≤0；当x∈（x0，x0＋δ）时f′（x）≥0，则f（x）在点x0取极小值；
（2）当x∈（x0－δ，x0）时，f′（x）≥0；当x∈（x0，x0＋δ）时f′（x）≤0，则f（x）在点x0取极大值.
证 （1）说明f（x）在（x0－δ，x0）内单调递减，而在（x0，x0＋δ）内单调递增.又f（x）在x0连续，故对任何x∈U（x0，δ），有
f（x）≥f（x0），
即f（x）在x0取极小值.
（2）类似可说明f（x）在x0取极大值.
注意 此定理只要求f（x）在x0连续，并未要求f（x）在x0可导.
定理4（极值的第二充分条件） 设f（x）在x0的某邻域U（x0，δ）内可导，在点x0处二阶可导，且f′（x0）＝0，f″（x0）≠0.
（1）若f″（x0）＜0，则f（x）在x0处取极大值；
（2）若f″（x0）＞0，则f（x）在x0处取极小值.
证 利用f（x）在x0处的泰勒公式
有
等式右边第二项为较第一项高阶的无穷小，从而在x充分靠近x0时，右边第一项的绝对值较大，它决定右边两项和的符号.即对x0的充分小的邻域U（x0）内的任何x：
（1）若f″（x0）＞0，则等式右边也大于0，从而有f（x）＞f（x0），则函数f（x）在x0取极小值；
（2）若f″（x0）＜0，则等式右边也小于0，从而有f（x）＜f（x0），则函数f（x）在x0取极大值.
费马定理说明：若函数在可导点x0取极值，则x0必为驻点，从而知函数的极值点只可能在不可导点与驻点中产生.极值的第二充分条件是判断驻点是否为极值点的有力工具.
例4 求f（x）＝（x－1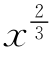
的极值.
解 f′（x）＝
这样得到函数f（x）的不可导点x1＝0和驻点x2＝
，利用极值的第一充分条件可求出极值，列表如下.
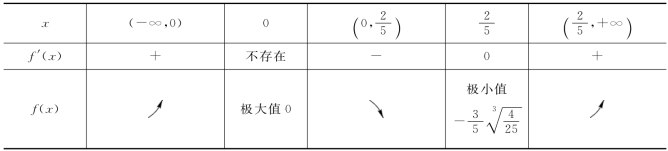
对x2＝
还可用第二充分条件来判断.
因为
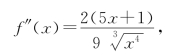
有
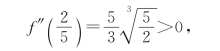
从而知f（x）在x2＝
取极小值，且极小值