二、分部积分法
用两个函数乘积的求导法可推出又一种重要的积分方法——分部积分法.
定理3 若u（x），v（x）均可导，不定积分∫u′（x）v（x）dx存在，则∫u（x）v′（x）dx也存在，并有
∫u（x）v′（x）dx＝u（x）u（x）－∫u′（x）v（x）dx.
证 由于［u（x）v（x）］′＝u′（x）v（x）＋u（x）v′（x）
所以
u（x）v′（x）＝［u（x）v（x）］′－u′（x）v（x），
两端积分，有
∫u（x）v′（x）dx＝u（x）v（x）－∫u′（x）v（x）dx.
例13 求∫arctan xdx，∫arcsin xdx.
解 设u（x）＝arctan x，v（x）＝x.
则
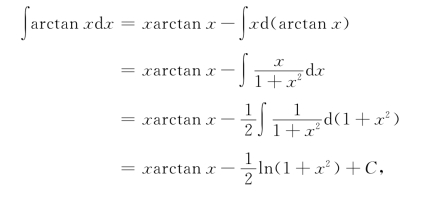
同理，有
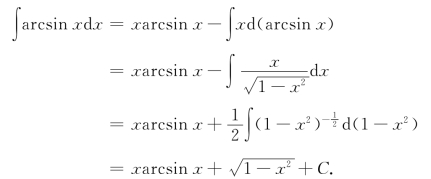
用类似的方法还可求得
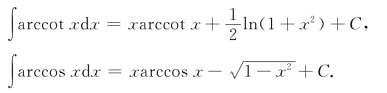
例14 求∫ln xdx.
解
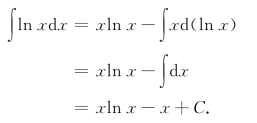
例15 求∫xexdx.
解
例16 求∫x2sin xdx.
解
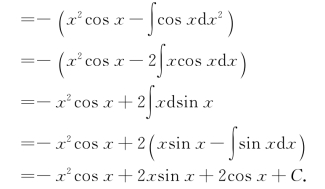
例17 求∫xln xdx.
解
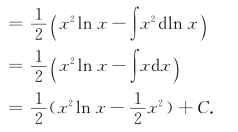
例18 求∫excos xdx，∫exsin xdx.
解 （方法一） 设I＝∫excos xdx，J＝∫exsin xdx.
则
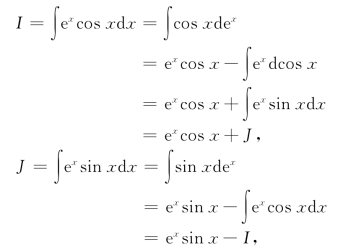
从而有
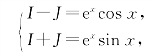
解此方程组，得
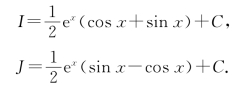
这种积分法称为“配对积分法”.
（方法二） 设
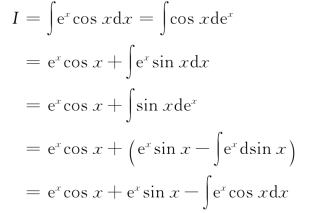
从而有
类似可求得
这种方法的特点是运算过程中又出现了所求的不定积分，通过求解关于所求不定积分的方程得出答案.
这种方法称为“循环法”.
例19 导出不定积分In＝∫
（n为自然数）（a＞0）的递推公式.
解 由于In＝
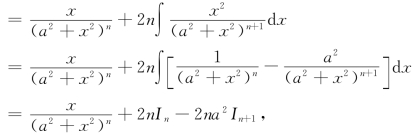
则有如下递推公式
由于I1＝∫
arctan
＋C，对任何自然数n，由以上递推公式总可求出I.
n这种积分法称为“递推法”.
到此为止，又有一些积分公式加入积分表中，请读者熟记.列举如下：
（1）∫tan xdx＝－ln｜cos x｜＋C；
（2）∫cot xdx＝ln｜sin x｜＋C；
（3）∫sec xdx＝ln｜sec x＋tan x｜＋C；
（4）∫csc xdx＝ln｜csc x－cot x｜＋C；
（5）∫
＋C；
（6）∫
＋C；
（7）∫
（8）∫
＋C；
（9）∫arcsin xdx＝xarcsin x＋
＋C；
（10）∫arccos xdx＝xarccos x－
＋C；
（11）∫arctan xdx＝xarctan x－
ln（1＋x2）＋C；
（12）∫arccot xdx＝xarccot x＋
ln（1＋x2）＋C.
对于一个初等函数，总可以求出它的导数，但求其不定积分就不一定那么容易，甚至有些初等函数的不定积分不是初等函数.在这个意义下，也就是并非所有初等函数的不定积分都是可以“求出来”的.
例如，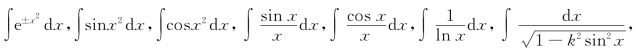
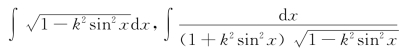（0＜k＜1）等积分在诸多领域中有着重要的应用，但均不为初等函数.掌握不定积分的大量运算技巧对今后的学习是必不可少的，但过分追求一些类似以上积分的特殊技巧，其效果显然会适得其反.